综合能源系统最优电力潮流（OPF）模型建立与Gurobi实现

日期：2024-05-06 05:10 / 作者：佚名

最优电力潮流（Optimal Power Flow，以下简称OPF）指当电网结构参数和负荷情况都已给定时，调节可利用的控制变量(如发电机输出功率、可调变压器抽头等)来找到能满足所有运行约束条件的，并使系统的某一性能指标(如发电成本或网络损耗)达到最优值下的潮流分布（来自百度百科）。

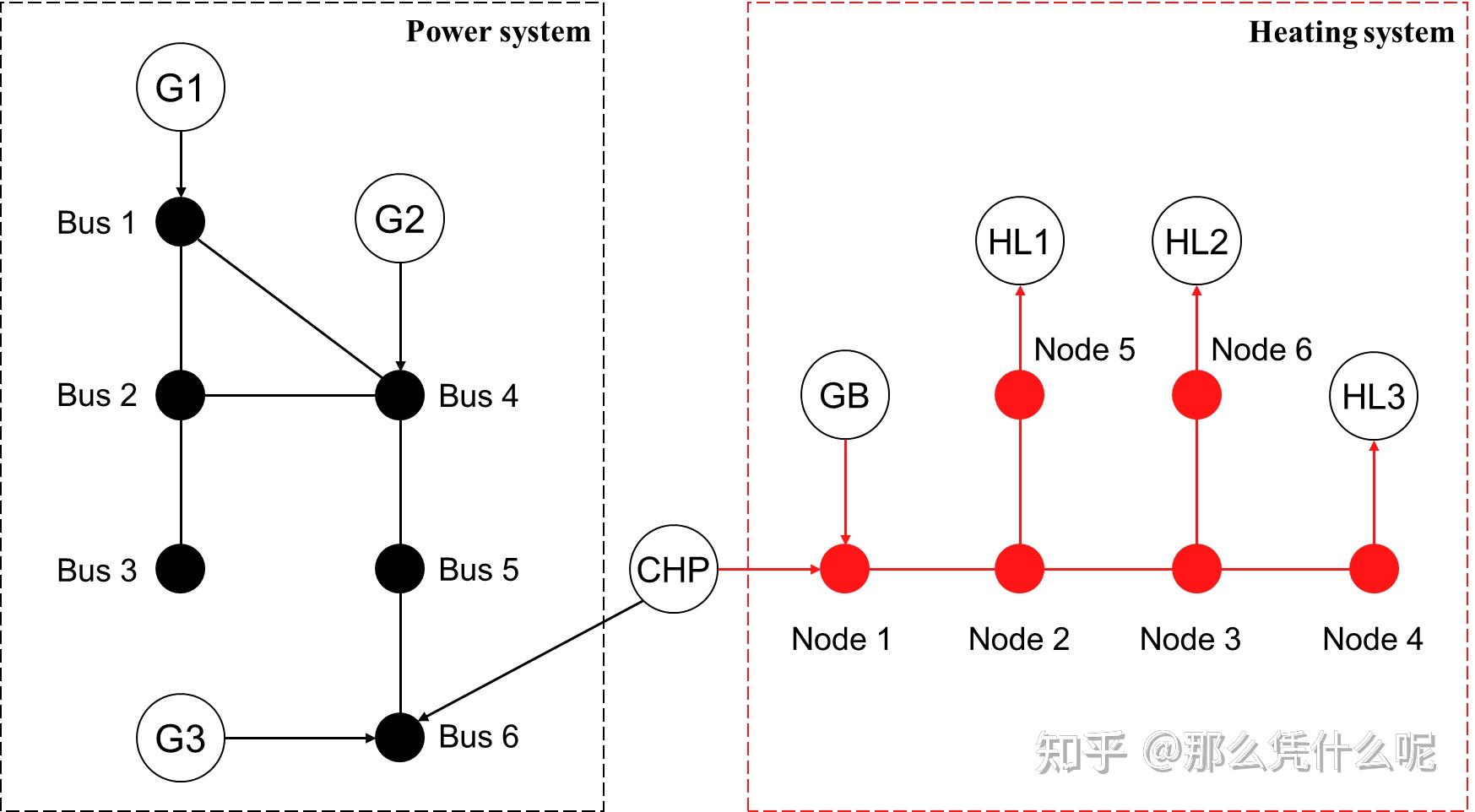
如下图所示，以我们研究的case为例，其OPF问题可以描述为：在一个优化调度时刻，各个节点的负荷需求是已知的，如何调节三台发电机和一台热电联产机组的输出电功率，使得电力系统能够在满足各负荷需求的前提下最小化发电成本。

从本质上来说，OPF模型的核心部分是由一系列描述节点能量流动状态的方程组构成的。具体来说，电网中的每个节点都需要满足能量守恒方程，即注入节点的总有功功率（或无功功率）需要等于从节点流出的总有功功率（或无功功率）。

但是，原始的最优潮流模型是非凸优化模型（推导可见电力领域经典教材《电力系统分析》），是Gurobi等主流商用求解器无法优化的复杂模型。因此，许多学者都对模型进行了简化或松弛，使得该问题能够在多项式时间内进行求解。常见的简化模型包括：直流最优潮流模型（DC-OPF）^[1]，基于二阶锥规划（SOCP）的最优潮流模型^[2]，基于半正定规划（SDP）的最优潮流模型^[3]等。详细介绍可见李博士的知乎文章：

菜鸟的能源优化之：基于Distflow的最优潮流模型(OPF)--模型推导篇

本专栏采用的模型是DC-OPF模型，它的优点是模型简单、求解速度快，但是精度是诸多简化模型中精度最低的。

DC-OPF模型仅仅考虑有功功率和电压相角，忽略了无功功率和电压。对于节点 $j$ ，其能量守恒方程如下所示：

$\\sum_{i:i\\rightarrow j}^{}{P_{ij}}+\\sum_{j}^{}{P_{j}^{G}}=\\sum_{k:j\\rightarrow k}^{}{P_{jk}}+P_{j}^{L}\\\\$

式中， $i:i\\rightarrow j$ 代表有功功率从节点 $i$ 流向该节点的集合， $k:j\\rightarrow k$ 代表有功功率从该节点流向节点 $k$ 的集合， $P_{ij}$ 代表从节点 $i$ 流向该节点的有功功率， $P_{jk}$ 代表从该节点流向节点 $k$ 的有功功率， $\\sum_{j}^{}{P_{j}^{G}}$ 代表所有该节点所有由发电设备所产生的有功功率， $P_{j}^{L}$ 代表该节点的有功负荷。注：当考虑储能设备时，由于储能既可以储电也可以放电，因此它可以存在于等式的两侧。

在DC-OPF模型下，节点间流动的有功功率由两节点间的相角差决定，如下式所示：

$P_{ij}^{}=\\frac{\ heta_{i}-\ heta_{j}}{x_{ij}}\\\\$

式中， $\ heta$ 为节点的相角， $x_{ij}$ 为两节点之间的电抗。

一个最简单粗暴的代码实现方法就是手动地把每个节点的方程都列出来，但是当节点数量很大时，巨大的工作量会让你崩溃。仔细观察可以发现，电网拓扑本质上是一个图，可以采用邻接矩阵的方法来统一地表示节点间的连接关系。具体思路如下：

参考matpower的电网数据输入格式，电网拓扑数据包含了节点（bus）信息、边（branch）信息、发电机（generator）信息等。原则上我们需要一个存储节点信息的数组和一个存储边信息的数据，不过由于我们采用的是DC-OPF模型，对于节点数组只需要存储各节点的有功负荷信息，因此可以省略掉。节点数组的数据结构如下：

# Branch of power line
# Content: from node, to node, reactance
# Unit:    none,      none,    p.u.
br_p = np.array([[1, 2, 0.17],
                [1, 4, 0.258],
                [2, 3, 0.197],
                [2, 4, 0.018],
                [3, 6, 0.037],
                [4, 5, 0.037],
                [5, 6, 0.14]])

br_p 是一个储存了电网边信息的数组，第一列和第二列分别表示边的起始节点和最终节点，第三列表示该边的电抗。通过定义一个生成邻接矩阵的函数，我们就可以把br_p转换为一个邻接矩阵数组。其中，若节点 $i$ 和 $j$ 有连接，则该数组的第 $i$ 行第 $j$ 列的值为电抗的倒数，否则，值为0。函数代码如下：

def generateXmatrix(n_bus, br_p):
    X=np.zeros((n_bus, n_bus))
    for branch in br_p:
        X[branch[0].astype(int) - 1][branch[1].astype(int) - 1]=1 / branch[2]
    return X

函数很简单，首先生成一个以节点个数为阶的全0方阵，然后按照上述规则赋值就好。这里稍微解释一下astype(int)，br_p中的数据格式为浮点数，没法直接X[][]中，因此通过它强制转为整数。通过该函数，我们就可以生成邻接矩阵数组，然后轻松地添加起各个节点的潮流约束，代码如下：

# 前置代码
m=Model('Optimal scheduling of the tested IES')
p_g1=m.addVar(lb=g_list[0][4], ub=g_list[0][5], name='power output of generator 1')
p_g2=m.addVar(lb=g_list[1][4], ub=g_list[1][5], name='power output of generator 2')
p_g3=m.addVar(lb=g_list[2][4], ub=g_list[2][5], name='power output of generator 3')
angle=m.addVars(n_bus, vtype=GRB.CONTINUOUS, lb=lb_angle, ub=ub_angle, name='voltage angle from bus 1 to bus 6')
m.addConstr(angle[0]>=0)
m.addConstr(angle[0]<=0)
p_chp=m.addVar(lb=lb_chp, ub=ub_chp, name='power output of CHP')
el=np.array([50, 50, 50, 50, 50, 50])
# 重组数据
p_g_set=np.array([p_g1, p_g2, 0, 0, 0, p_g3])
p_chp_set=np.array([0, 0, 0, 0, 0, p_chp])
# 生成邻接矩阵
X=generateXmatrix(n_bus, br_p) #  n_bus=6

# 核心代码
m.addConstrs(sum(X[j][i]* (angle[j]- angle[i]) for j in range(n_bus)) + p_g_set[i]/ BASE_P + p_chp_set[i]/ BASE_P==     sum(X[i][j]* (angle[i]- angle[j]) for j in range(n_bus)) + el[i]/ BASE_P for i in range(n_bus))

详细的解释一下这段代码：

line 3-5：添加三台发电机的出力变量
line 6-8：添加各个节点的相角变量，其中节点1的相角为基准点，固定为0
line 9：添加CHP机组的电出力变量
line 10：设置各节点的有功负荷
line 12-13：按照节点顺序重新组织各出力在各个节点中的位置（注：这里其实可以优化一下，让它自动生成，不过想了一下稍微有点麻烦，就懒得写了）
核心代码段：首先看整体， $i$ 代表一个大循环，每一个循环对应生成一个节点的潮流约束， $j$ 代表一个小循环，即对于节点i，遍历所有与它相邻的节点 $j$ （包括了以节点j为起点的情况，即第一个sum，和以节点 $j$ 为终点的情况，即第二个sum），sum里是根据节点连接情况计算的节点间流动的功率。其他的电出力和电负荷，分别添加在等式的左右两侧。

这样，电网部分代码就已经写好了。下一篇将介绍如何建立OTF的模型以及其高效的代码实现。