

高级加密标准(英语:Advanced Encryption Standard,缩写:AES),又称Rijndael加密法(荷兰语发音: [?r?inda?l],音似英文的“Rhine doll”),是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES,已经被多方分析且广为全世界所使用。经过五年的甄选流程,高级加密标准由美国国家标准与技术研究院(NIST)于2001年11月26日发布于FIPS PUB 197,并在2002年5月26日成为有效的标准。现在,高级加密标准已然成为对称密钥加密中最流行的算法之一。
该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计,结合两位作者的名字,以Rijndael为名投稿高级加密标准的甄选流程。
| 密钥长度 | 128、192、156bit |
|---|---|
| 分组长度 | 128bit |
| 结构 | 置换排列网络 |
| 重复回数 | 10、12、14等(视密钥长度而定) |
关系密码攻击可以破解9个加密循环/256比特(密钥)的AES。另外选择明文攻击可以破解8个加密循环,192或256比特(密钥)的AES,或7个加密循环、128位(密钥)的AES。
严格地说,AES和Rijndael加密法并不完全一样(虽然在实际应用中两者可以互换),因为Rijndael加密法可以支持更大范围的区块和密钥长度:AES的区块长度固定为128比特,密钥长度则可以是128,192或256比特;而Rijndael使用的密钥和区块长度均可以是128,192或256比特。加密过程中使用的密钥是由Rijndael密钥生成方案产生。
大多数AES计算是在一个特别的有限域完成的。
AES加密过程是在一个4×4的字节矩阵上运作,这个矩阵又称为“体(state)”,其初值就是一个明文区块(矩阵中一个元素大小就是明文区块中的一个Byte)。(Rijndael加密法因支持更大的区块,其矩阵的“列数(Row number)”可视情况增加)加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:
代码流程图如下图:
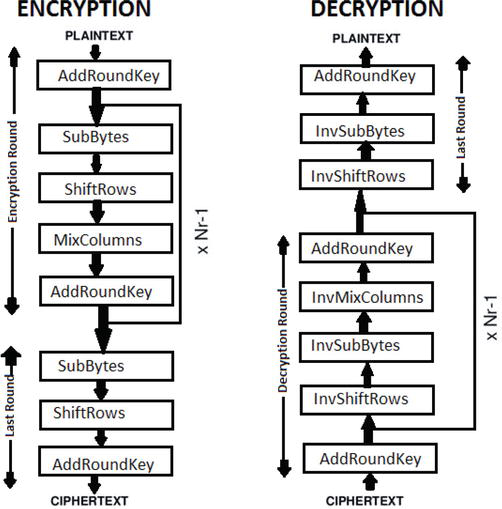
对应的c语言代码如下:
解谜操作与加密操作相反,
步骤,回合密钥将会与原矩阵合并。在每次的加密循环中,都会由主密钥产生一把回合密钥(通过Rijndael密钥生成方案产生),密钥大小会跟原矩阵一样,与原矩阵中每个对应的字节作XOR操作。
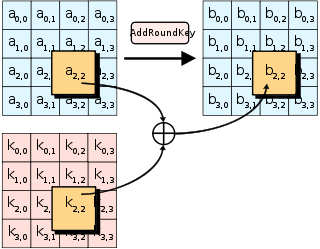
对应的c代码如下:
在步骤中,矩阵中的各字节通过一个8位的 S-box 进行转换。这个步骤提供了加密法非线性的变换能力。S-box 与 $GF(2^8)$ 上的乘法逆元有关,已知具有良好的非线性特性。为了避免简单代数性质的攻击,S-box结合了乘法逆元及一个可逆的仿射变换矩阵建构而成。此外在建构S-box时,刻意避开了不动点与反不动点,即以S-box替换字节的结果会相当于错排的结果。
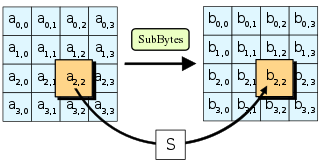
对应的c代码:
AES算法的 S-box:
描述矩阵的列操作。在此步骤中,每一列都向左循环位移某个偏移量。在AES中(区块大小128位),第一列维持不变,第二列里的每个字节都向左循环移动一格。同理,第三列及第四列向左循环位移的偏移量就分别是2和3。128位和192比特的区块在此步骤的循环位移的模式相同。经过之后,矩阵中每一竖行,都是由输入矩阵中的每个不同行中的元素组成。Rijndael算法的版本中,偏移量和AES有少许不同;对于长度256比特的区块,第一列仍然维持不变,第二列、第三列、第四列的偏移量分别是1字节、2字节、3字节。除此之外,操作步骤在Rijndael和AES中完全相同。
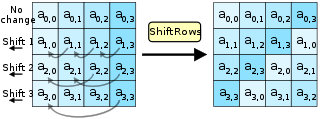
对应的c代码:
在步骤,每一列的四个字节通过线性变换互相结合。每一列的四个元素分别当作${\displaystyle 1,x,x{2},x{3}}$ 的系数,合并即为 ${\displaystyle GF(2^{8})}$ 中的一个多项式,接着将此多项式和一个固定的多项式 ${\displaystyle c(x)=3x{3}+x+x+2}$ 在模 ${\displaystyle x^{4}+1}$ 下相乘。此步骤亦可视为Rijndael有限域之下的矩阵乘法。函数接受4个字节的输入,输出4个字节,每一个输入的字节都会对输出的四个字节造成影响。因此和两步骤为这个密码系统提供了扩散性。
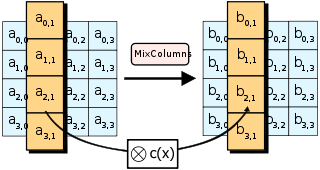
对应c代码:
Rijndael的作者曾经为该算法提供了一个[主页](IAIK Krypto Group - AES Lounge (archive.org))。
现在这个主页的内容已经扩充了许多内容:
包括一些分析AES安全性的论文、AES硬件实现、高速AES实现、低代价AES实现、软件实现、侧信道分析、出错分析、AES扩展指令集等等内容。
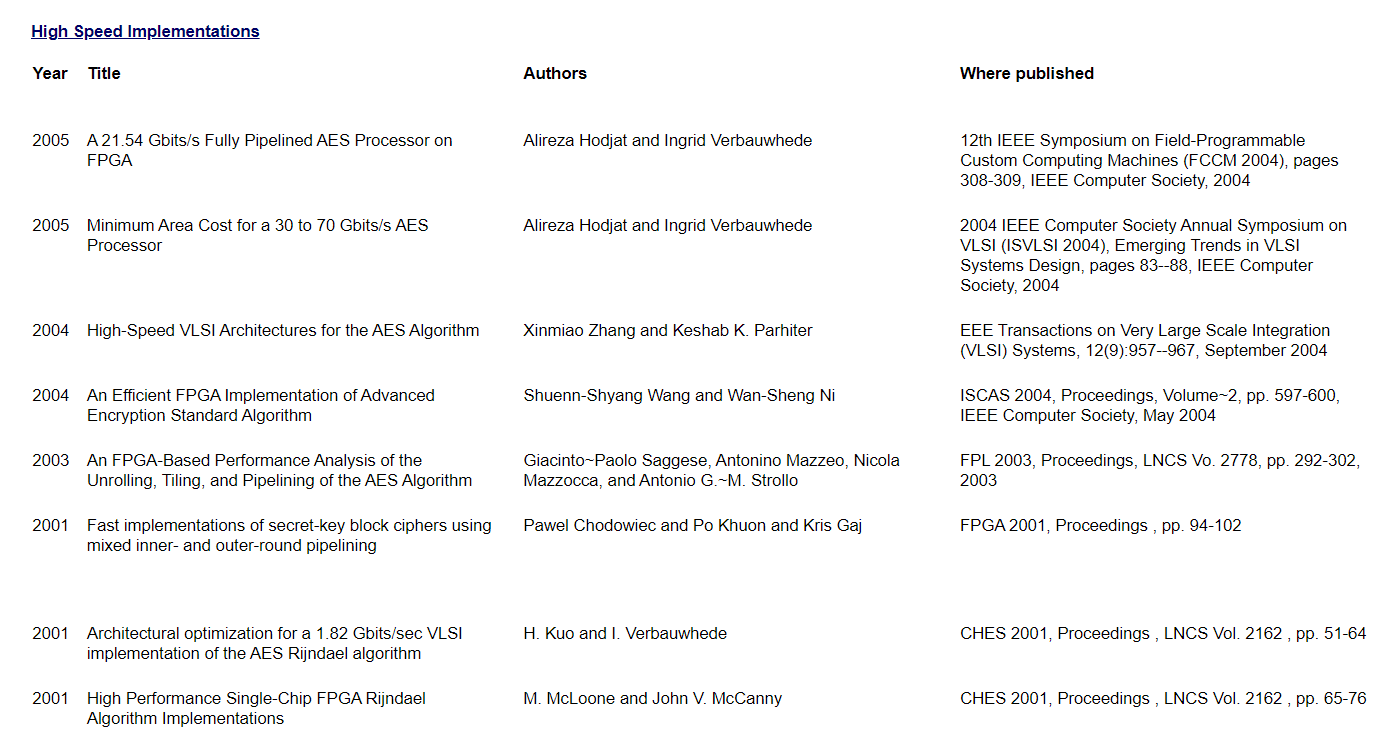
可以看到AES加密速率从2001年的1.82Gbits/sec发展到2005年21.54Gbits/sec以及70Gbits/sec,发展非常迅速,大多都是使用FPGA在硬件算法实现层面进行的优化。

在侧信道分析部分可以看到经典的论文,比如AES高阶掩码,功率分析等等。有机会可以看一看。
在软件中实现AES时应该小心,特别是围绕侧通道攻击。
对较短的块进行加密只能通过填充源字节(通常使用空字节)来实现。
分组密码有五种工作体制:
这种模式是将整个明文分成若干段相同的小段,然后对每一小段进行加密。
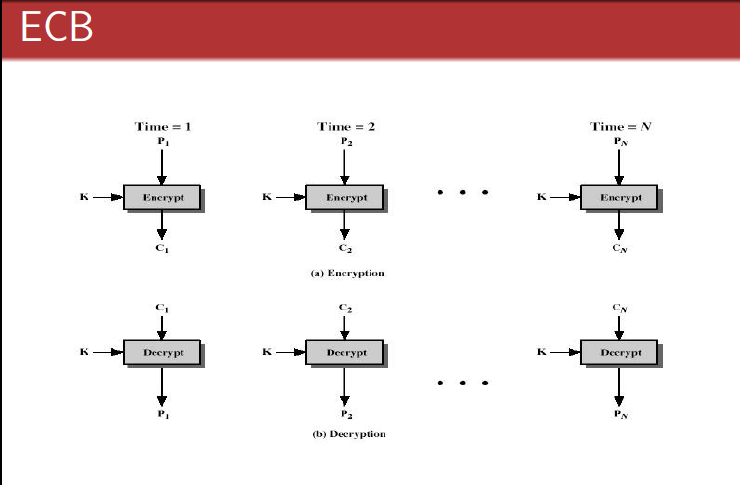
这个方法很简单,但是不安全,因为保留了明文的结构信息。
对应的c代码实现:
这种模式是先将明文切分成若干小段,然后每一小段与初始块或者上一段的密文段进行异或运算后,再与密钥进行加密。
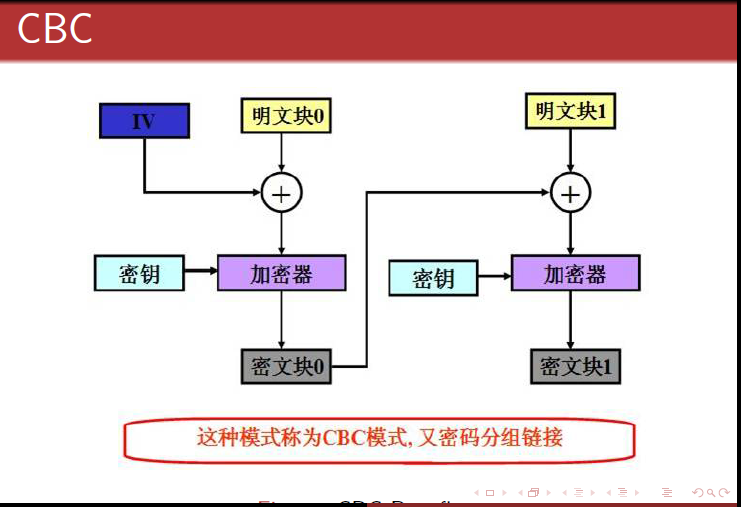
对应c实现:
计算器模式不常见,在CTR模式中, 有一个自增的算子,这个算子用密钥加密之后的输出和明文异或的结果得到密文,相当于一次一密。这种加密方式简单快速,安全可靠,而且可以并行加密,但是在计算器不能维持很长的情况下,密钥只能使用一次。CTR的示意图如下所示:
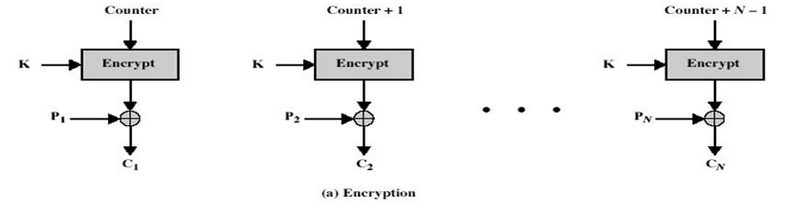
对应的c代码:
其他两种比较复杂,不再详细说明、也没有写相应的代码。
使用32或更多比特寻址的系统,可以事先对所有可能的输入创建对应表,利用查表来实现,和步骤以达到加速的效果。这么做需要产生4个表,每个表都有256个格子,一个格子记载32位的输出;约占去4KB(4096字节)存储器空间,即每个表占去1KB的存储器空间。如此一来,在每个加密循环中,只需要查16次表,作12次32位的XOR运算,以及AddRoundKey步骤中4次32位XOR运算。若使用的平台存储器空间不足4KB,也可以利用循环交换的方式一次查一个256格32位的表。参考文章:Efficient Software Implementation of AES on 32-Bit Platforms | SpringerLink
使用一种面向字节的方法,即从字节的角度分析,可以将, , 三个步骤合为一个操作。参考资料中也给出了相应的论文和实现。
这种优化面向嵌入式设备,因为设备内存通常不足4KB。实际上这种优化目前已经有人完成、并且将所有的查找表替换为了实时计算。参考资料7中有详细的描述。
这项工作在2003年由Bertoni等人完成,它们在低内存嵌入式设备中仅仅使用Sbox和InvSbox的情况下对AES算法进行了优化。详细内容见参考资料9,11。
算法的关键是使用了明文矩阵的转置。

这个操作非常简单,但是有一些非常有趣的结果。
结果是 , , 与之前的操作时类似的,但是通过这个转置运算可以被极大地加速。
在旧的 中,操作是这样的,实际上是 $GF(2^8)$ 上的矩阵乘法:

每一列代价为4次乘法,4次XOR加法,3次移位操作。
总代价为 16次 $GF(2^8)$ 乘法,16次加法,12次移位以及一个中间变量。
新的 操作:
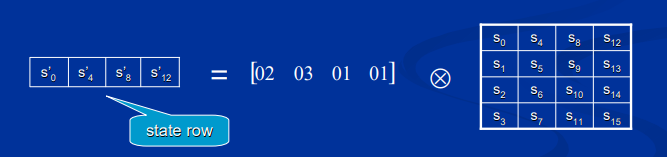
区别在于以行来处理state数组而不是按列处理。
新的 需要16次乘法和16次XOR运算,不需要其他操作。
解密与加密类似,详细内容查看参考资料9和11。
理论上来讲这种方法的速度最快(如果将上面的优化结合起来应该会更快,由于时间限制,不能写出完整的代码),但是并不安全,优化的核心是将运算过程用查表的方式实现,以下是用到的几个查询表:
分别是Sbox和Sbox的逆
Xtime2Sbox这个表是Xtime2和Sbox的组合,即Xtime2[Sbox[]],Xtime3Sbox同理,在加密过程中用来做有限域中的乘法,在上面的算法说明中有解释。
在解密时使用,用于有限域乘法,是加密多项式的乘法逆元。
在这个角度上,加密函数可以写为:
操作的查表实现:
的查表实现:
这个函数将 三个函数结合在一起,其中XtimeXSbox[]等于XtimeX[Sbox[]]。
操作与前面的算法是一致的:
与加密类似,解密也采用查表实现。
实现:
实现:
然而,实际实现中应避免使用这样的对应表,否则可能因为产生缓存命中与否的差别而使侧信道攻击成为可能。
这一部分详细资料在参考资料12,即Intel AES-NI白皮书。
利用硬件指令的优化是软件实现的降维打击,可以做到 $1.3 cycles/sec$,甚至可以做到 $0.36cycles/sec$。
在Crypo++官方benchmark例程中,CTR模式AES速度轻松达到 $4400Mb/sec$ 。在参考资料中给出了crypo++的源代码,试着阅读之后,由于时间关系还是放弃了分析。
下面是基本没有优化的使用AES-NI实现的AES算法,首先是加密函数:
解密函数:
以CPU周期数为计量单位,仅仅使用Sbox加解密时,测试的结果如下:
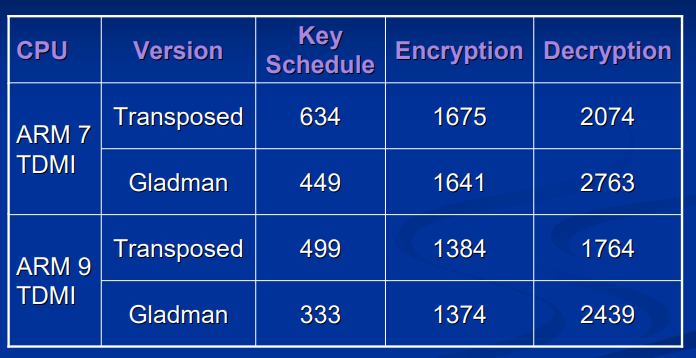
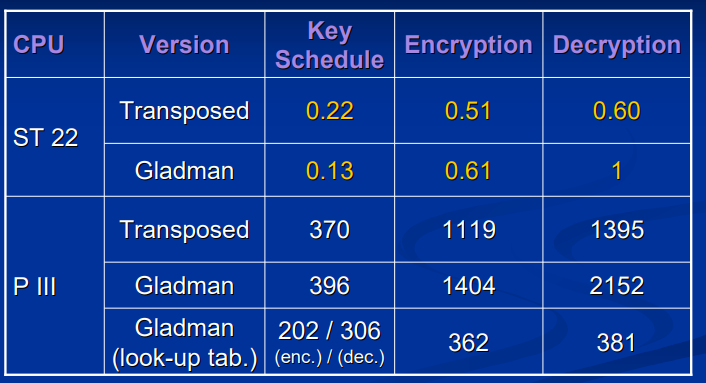
与 Gladman 给出的算法的对比:
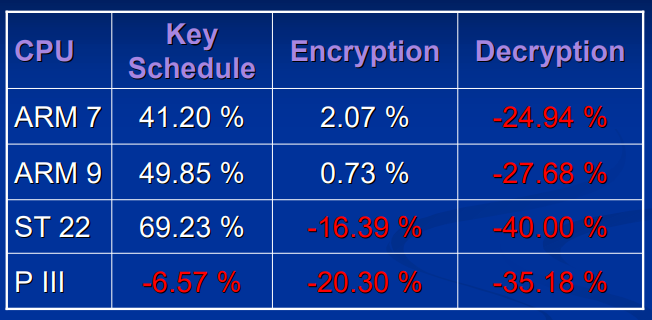
可以看到算法在解密方面提升很大。

经过五次运行测试,取平均值最终得到的结果如下:
| 加密时间(CPU cycle) | 解密时间(CPU cycle) |
|---|---|
| 73 | 111 |
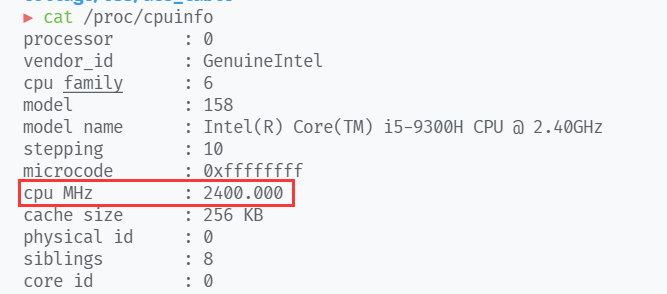
测试的CPU为 ,主频2400MHz。
加密速率 $ES=cpu_{fre}/t_{encrypt}=2400 * 10^6/73=32.88 * 10^6bytes/sec$
解密速率 $DS=cpu_{fre}/t_{decrypt}=2400*106/111=21.62*106bytes/sec$

6.04452s内完成了789949975次AES操作。
加密速率 $ES=789949975/6.04452*16bytes/sec=1994.15Mb/s$
通过读取随机文件得到的结果:
用 命令生成随机文件。

这里读取随机文件大小为16MB,速率为 ,但是使用 函数测量会导致结果不准确,然而使用 汇编指令出现了一些问题。可能由于解密速率过大,导致 函数两次返回值相同。
所以将设置文件大小为168MB,再次运行:

加密速率为 $3902.44Mb/s$
解密速率为 $2711.86Mb/s$
多次运行,加密速率最高达到 $4705.88Mb/s$

多次运行,解密速率最高达到 $4102.56Mb/s$
