

轨迹规划一般指在空间路径上附加运动学、动力学约束,然后确定每个路径点的速度、加速度信息。在论文上看到转弯的轨迹有clothoid,polar polynomials,bezier poly nomial,但是都没有讲如何给这些曲线添加速度信息。我了解到速度一般用梯形速度曲线,不知道这个过程是不是叫速度规划。如何实现给路径添加速度信息这个过程呢?
摘要:运动规划是移动机器人自主导航系统中的重要模块之一,相关算法研究成果层出不穷,本文将曲线插值拟合算法拆解为三个子类算法:基于插值的规划算法、基于特殊曲线的规划算法及基于优化的规划算法,并沿时间顺序概述相关算法的发展历程,最后从模型复杂度、实时性、环境适应能力及路径曲线质量等方面分析了上述三类算法的优缺点。
01

引言

在前文《机器人图规划算法研究现状简述》中,结合图 1.1对“运动规划是什么?要解决什么问题?”这两个问题有详细阐述,并概述了运动规划与运动控制模型、环境感知这两个部分之间的关系。

图 1.1 运动规划示意图(图片来源:http://wiki.ros.org/navigation)
从上述可知,要进行运动规划,需要有两个前提条件:地图和定位。机器人需要先利用传感器获取环境信息,构建环境地图并计算自身在环境地图中的位姿(见《机器人环境感知研究现状简述》),接着根据自身在地图中的位置,明确起始点和终点后,才可以进入到运动规划阶段,最后将生成的轨迹转化为运动控制命令发送给运动控制模型(见《常见移动机器人运动学模型总结》),驱动机器人运动。
如图 1.2所示,运动规划的研究主要是对多目标多变量多约束耦合的规划模型优化求解。对于具有非完整约束的移动机器人而言(见《两轮差速驱动机器人运动模型及应用分析》),在分布有障碍物的环境中求解最优路径是NP-hard问题,即对于任意场景无法保证在多项式时间内求得最优解,因此大部分规划算法追求次优解或局部最优[1]。
诸多学者针对不同应用场景和需求,设计、改进了非常多的运动规划算法,其中常见的运动规划算法主要包括四类:图规划算法、空间采样算法、曲线插值拟合算法和仿生智能算法,通过规划模型求解得到最佳轨迹曲线,包含无碰撞顺滑的路径曲线和平滑的速度曲线,并输入到控制器驱动机器人运动。
本文将对曲线插值拟合算法领域的研究进展及成果进行分类阐述,主要概述同族算法的发展过程,不对具体算法展开分析,在后续系列文章会挑选部分经典常用算法深入剖析。
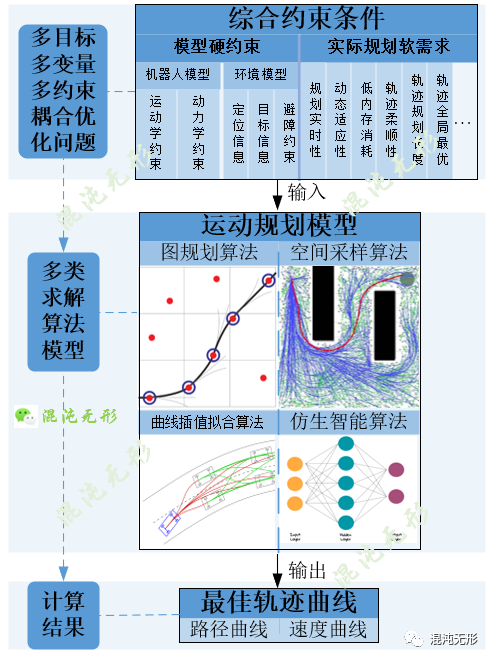
图 1.2 运动规划通用模型
02

曲线插值拟合算法研究分析

上述大部分《图规划算法》和《空间采样算法》生成的路径存在折点、急弯等曲率不连续的情况,影响了机器人运动平稳性,因此需要综合考虑模型硬约束与实际规划软需求,以提升路径平滑度。曲线插值拟合算法在曲线平滑控制及优化方面有显著的优势,按照曲线生成方式及其种类可分为:基于插值的规划算法、基于特殊曲线的规划算法及基于优化的规划算法三类,该类算法在自动驾驶等领域有着广泛的应用。
2.1
基于插值的规划算法
第一类是采用多项式曲线来描述机器人运动轨迹,这是因为多项式曲线灵活多变,且能容易满足曲率连续要求,并能够容易导出速度曲线,因此非常适合描述机器人运动轨迹,按照多项式构造方式主要分为:插值多项式曲线、贝塞尔曲线、样条曲线,具体如下:
Chang等人提出QPMI (Quadratic Polynomial and Membership Interpolation)算法可创建无碰撞、无龙格现象的曲率连续曲线,并使用Pan算法检测曲线碰撞点位置,并通过增加子锚点以重规划无碰撞路径,但在复杂拥挤环境下的碰撞检测及重规划成本较高[2]。
Werling等人基于道路建立Frenet坐标系,将无人车运动分解为纵向、横向运动,并分别建立路程-时间的五次多项式方程,考虑避障约束、舒适度等因素及其长期运动模式(换道、合并等)设计优化目标函数,结合始末运动状态,输出最佳运动控制量[3]。
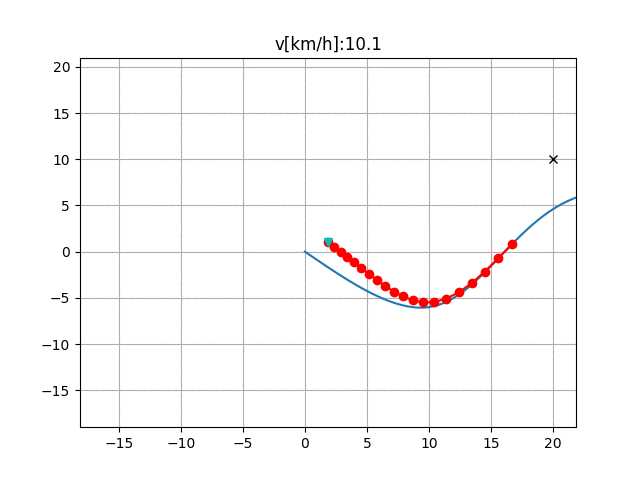
图 2.1 基于Frenet坐标系规划的多项式轨迹[3]
Xu等人进一步提出路径、速度解耦循环迭代优化框架,如图 2.2所示,将三次多项式(绿色)或五次多项式(红色)应用于道路状态网格,综合静态、动态成本函数,选择最佳轨迹,并以该最佳轨迹(包含路径、曲线)为初值,使用单纯形法循环迭代优化路径曲线(先)及速度曲线(后),比未使用该迭代优化框架的算法性能提升10%,规划时间减少50%[4]。

图 2.2 多项式路径曲线[4]
Talamino等人提出与文献[3, 4]相似的运动规划方法,作者基于Frenet坐标系横轴、纵轴分别用两个五次多项式曲线连接相邻状态,并分析得到该曲线及其曲率变化具有对称性,得到简洁的优化模型,极大提升路径曲线生成效率,并基于该曲线建立速度优化模型,最终在仿真中验证了无人车在避障、变道等场景的良好性能[5]。
Han等人综合局部栅格图中的全局路径及障碍物影响以确定控制点,生成无碰撞的四阶贝塞尔曲线作为局部路径,并使用PID控制器根据曲线[6]。
如图 2.3所示,González等人针对单岔口、连续岔口场景使用三阶贝塞尔曲线过渡,并提出曲率评估权重算法调节控制点以保证曲线曲率(起始点、终止点及中间段)连续且满足最大曲率约束,并被集成到RITS自动驾驶系统[7]。
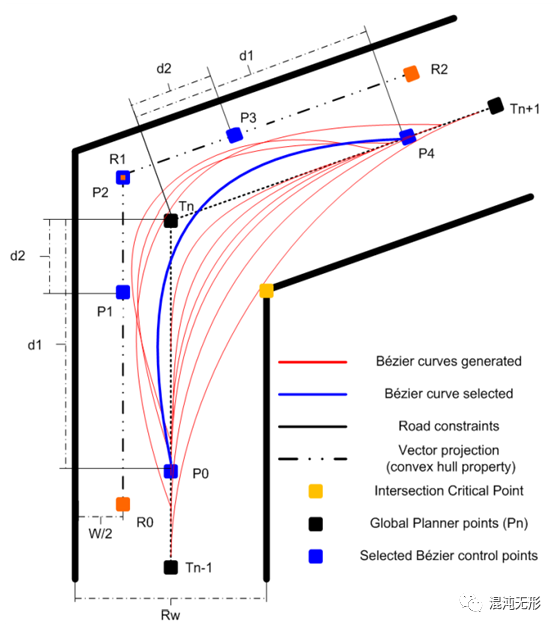
图 2.3 贝塞尔曲线[7]
Elbanhawi等人针对类车机器人提出B样条曲线与RRT相结合的方法,利用B样条曲线平滑性好的特点以降低搜索维度,快速生成适用于轮式机器人的曲率连续曲线[8]。
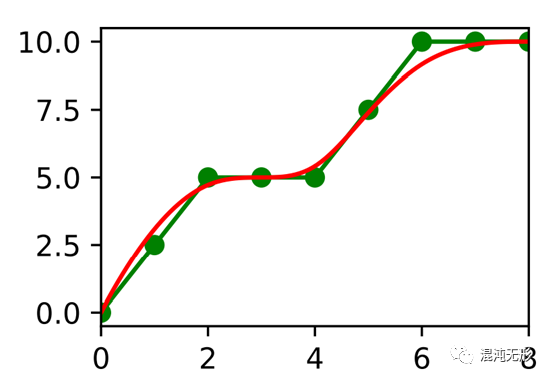
图 2.4 B样条曲线[8]
NURBS曲线是特殊的B样条曲线,Belaidi等人针对移动机器人在三维环境下的运动规划问题,采用NURBS曲线生成平滑的路径[9]。
2.2
基于特殊曲线的规划算法
第二类算法是采用特殊曲线描述规划的轨迹,特殊曲线规划主要包含了直线-圆弧曲线和Clothoid曲线两种。
其中直线-圆弧曲线是指针对类车机器人运动约束问题,在给定两个位置矢量,仅使用圆弧(满足最小曲率)和直线段合成最短平滑的路径,Dubins曲线限定机器人仅能前向运动。如图 2.5所示,R&S曲线将其拓展为双向运动,由于其简洁性而多被后续研究集成应用到其他算法,如Hybrid A*[10]使用R&S曲线条件改善路径质量,CL-RRT[11]使用Dubins距离提升采样点生成“良率”。

图 2.5 Dubins曲线[10]
Clothoid曲线的曲率随弧长线性变化,在轨迹平滑中极具优势,如Kim等人提出了一种基于Clothoid曲线的移动机器人运动规划算法,不仅缩短了路径长度,也降低了曲率变化量[12]。
2.3
基于优化的规划算法
第三类算法是主要是将多目标多变量多约束耦合的规划模型转化为有权重的惩罚函数,并优化求解,通常用于初始路径的平滑。
Ren等人针对势场法存在振荡等问题,将改进牛顿法优化方法应用于连续势场导航模型,并考虑了机器人非全向约束和移动障碍物影响,极大提升了系统性能,但存在优化计算成本较高的问题[13]。
Ratliff等人针对高维运动规划问题提出CHOMP(Covariant Hamilton Optimization Motion Planning)算法(图 2.6),先创建起始位置到终止位置的初始路径,针对成本函数使用梯度下降法对轨迹进行优化,获得平滑、无碰撞的轨迹,但存在容易陷入局部最小值的问题,因此引入了使用Hamilton Monte Carlo算法施加扰动,以重新启动优化过程,然而,引入了随机性,从而降低了优化结果的确定性。
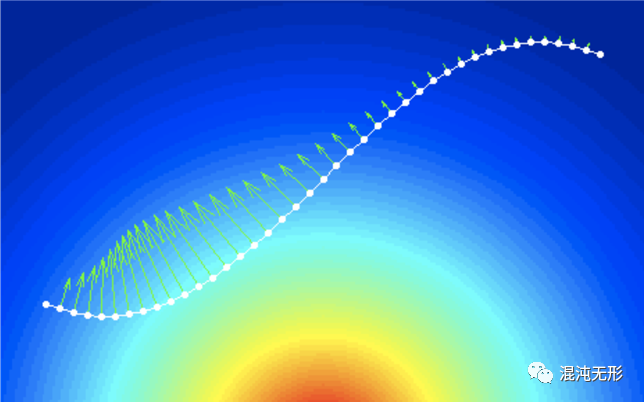
图 2.6 CHOMP[14]
与之相近,Kalakrishnan等人提出的STOMP (Stochastc Trajectory Optimization Motion Planning)算法不需要目标函数梯度信息,因此可提高机器人运动规划性能,通过生成带有噪声的轨迹探索初始轨迹周围的空间,以产生较低成本的轨迹。其随机性也克服了基于梯度方法存在的局部最小值问题[14]。
Dolgov等人使用Hybrid A*生成的初始路径,并以路径曲率最小化为目标,使用共轭梯度法优化得到平滑路径,并将存在碰撞情况的对应原始路径点作为锚点重新优化,以保证路径安全可靠[10]。
Ziegler等人提出一种局部连续的轨迹规划方法,通过结合道路边缘及障碍物将工作空间转化为凸空间,并引入连续可微的伪距离构建伪梯度场,综合模型硬约束及舒适性等要求,转化为带约束的非线性规划问题,并使用序列二次规划算法求解[15]。
Quinlan、R?smann、Magyar等人将“橡皮筋受内、外力作用产生形变”的原理应用于路径平滑处理,EB(Elastic Bands)[16]算法使用气泡带算法生成不连续的初始路径,再使用“橡皮筋”形变模型优化路径形状,生成无碰撞的平滑路径。TEB(Timed Elastic Band)[17]将静态、动态约束(速度、加速度等)和机器人状态使用稀疏图描述(强扩展特性),并转化为加权的单目标优化问题,并使用大规模最小二乘法求解,生成符合约束最低成本的轨迹(见图 2.7),具有极强的动态避障和重规划能力,并应用于多种类型的轮式机器人。DT-TEB(TEB in distinctive topologies)[18]将RRT算法、Voronoi图分别与TEB相结合,实时生成局部拓扑空间中全局最优轨迹,并延长了生成轨迹的长度,提高避障性能。CES(Convex Elastic Smoothing)[19]算法针对类车机器人运动规划模型,将气泡带初始路径形状“拉伸”优化及给定路径下速度优化问题构造为两个凸优化问题,并迭代优化路径曲线-速度曲线,实时生成平滑轨迹。

图 2.7 TEB算法[17]
03

曲线插值拟合算法分析

上述三类曲线插值拟合算法各有各的特点,接下来对比分析这三类规划算法的优缺点:
3.1
基于插值的规划算法
主要优点:易于计算,曲线形态灵活多变;
主要缺点:曲率连续性不保证
主要优点:计算成本低,控制点可产生期望的曲线,曲线间可相互连接;
主要缺点:高阶曲线难以调节,全局路径点影响整条曲线,控制点较难设置
主要优点:计算成本低,曲率连续易于保证,控制点容易控制曲线形状;
主要缺点:难以平衡曲线形状和连续性需求
3.2
基于特殊曲线的规划算法
主要优点:易于计算,且为最短路径;
主要缺点:路径的曲率不保证连续
主要优点:路径曲率变化线性,曲率连续性容易保证;
主要缺点:算法中的Fresnel积分难以计算
3.3
基于优化的规划算法
主要优点:各类软硬约束易于综合处理,曲线连续性易于保证;
主要缺点:优化变量越多,耗时越久,且易陷入局部最小值。
总体而言,基于插值拟合算法已经能够在诸多场景下的规划生成一条无碰撞路径,且应用较为广泛,比如TEB算法就被作为ROS navigation stack中local planner的算法之一,Dubins曲线或R&S曲线常被应用于自动泊车领域。随着诸多学者的改进升级,基于插值拟合算法的实时性和动态适应性逐渐提升,但多数算法仍存在优化计算容易陷入局部最小值、计算复杂等问题,但随着硬件计算能力的提升,相关算法已经被应用于实际。
04

结论与展望

本文将曲线插值拟合算法拆解为三个子类算法:基于插值的规划算法、基于特殊曲线的规划算法及基于优化的规划算法,并沿时间先后顺序概述了相关类型算法的发展改进历程,接着从模型复杂度、计算实时性、动态环境适应能力及路径曲线质量等方面分析了上述三类算法的优缺点,并指出存在的相关问题。
运动规划算法种类繁多,应用场景各不相同,而本文仅概述分析了四类运动规划算法之一的曲线插值拟合算法,后续会分析其他类型算法。
(文章仅笔者个人分析,有误请指正,谢谢!)
参考资料
[1]REIF J, WANG H. The complexity of the two dimensional curvature-constrained shortest-path problem; proceedings of the Third International Workshop on Algorithmic Found
[2]CHANG S-R, HUH U-Y. A collision-free G 2 continuous path-smoothing algorithm using quadratic polynomial interpolation[J]. International Journal of Advanced Robotic Systems, 2014, 11(12): 194.
[3]WERLING M, KAMMEL S, ZIEGLER J, et al. Optimal trajectories for time-critical street scenarios using discretized terminal manifolds[J]. The International Journal of Robotics Research, 2012, 31(3): 346-59.
[4]XU W, WEI J, DOLAN J M, et al. A real-time motion planner with trajectory optimization for autonomous vehicles; proceedings of the 2012 IEEE International Conference on Robotics and Automation, F, 2012[C]. IEEE.
[5]TALAMINO J P, SANFELIU A. Anticipatory kinodynamic motion planner for computing the best path and velocity trajectory in autonomous driving[J]. Robotics and Autonomous Systems, 2019, 114(93-105.
[6]HAN L, YASHIRO H, NEJAD H T N, et al. Bezier curve based path planning for autonomous vehicle in urban environment; proceedings of the 2010 IEEE Intelligent Vehicles Symposium, F, 2010[C]. IEEE.
[7]GONZáLEZ D, PéREZ J, LATTARULO R, et al. Continuous curvature planning with obstacle avoidance capabilities in urban scenarios; proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), F, 2014[C]. IEEE.
[8]ELBANHAWI M, SIMIC M, JAZAR R. Randomized bidirectional B-Spline parameterization motion planning[J]. IEEE Transactions on intelligent transportation systems, 2015, 17(2): 406-19.
[9]BELAIDI H, HENTOUT A, BOUZOUIA B, et al. NURBs trajectory generation and following by an autonomous mobile robot navigating in 3D environment; proceedings of the The 4th Annual IEEE International Conference on Cyber Technology in Automation, Control and Intelligent, F, 2014[C]. IEEE.
[10]DOLGOV D, THRUN S, MONTEMERLO M, et al. Path planning for autonomous vehicles in unknown semi-structured environments[J]. The International Journal of Robotics Research, 2010, 29(5): 485-501.
[11]KUWATA Y, TEO J, FIORE G, et al. Real-time motion planning with applications to autonomous urban driving[J]. IEEE Transactions on Control Systems Technology, 2009, 17(5): 1105-18.
[12]KIM Y, PARK J B, SON W, et al. Modified turn algorithm for motion planning based on clothoid curve[J]. Electronics Letters, 2017, 53(24): 1574-6.
[13]REN J, MCISAAC K A, PATEL R V. Modified Newton's method applied to potential field-based navigation for nonholonomic robots in dynamic environments[J]. Robotica, 2008, 26(1): 117-27.
[14]KALAKRISHNAN M, CHITTA S, THEODOROU E, et al. STOMP: Stochastic trajectory optimization for motion planning; proceedings of the 2011 IEEE international conference on robotics and automation, F, 2011[C]. IEEE.
[15]ZIEGLER J, BENDER P, DANG T, et al. Trajectory planning for Bertha—A local, continuous method; proceedings of the 2014 IEEE intelligent vehicles symposium proceedings, F, 2014[C]. IEEE.
[16]QUINLAN S, KHATIB O. Elastic bands: Connecting path planning and control; proceedings of the[1993]Proceedings IEEE International Conference on Robotics and Automation, F, 1993[C]. IEEE.
[17]R?SMANN C, FEITEN W, W?SCH T, et al. Trajectory modification considering dynamic constraints of autonomous robots; proceedings of the ROBOTIK 2012; 7th German Conference on Robotics, F, 2012[C]. VDE.
[18]R?SMANN C, HOFFMANN F, BERTRAM T. Integrated online trajectory planning and optimization in distinctive topologies[J]. Robotics and Autonomous Systems, 2017, 88(142-53.
[19]ZHU Z, SCHMERLING E, PAVONE M. A convex optimization approach to smooth trajectories for motion planning with car-like robots; proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), F, 2015[C]. IEEE.ations of Robotics, F, 1998[C].
福利放送
笔者为小伙伴们整理了期刊论文版式原文PDF,方便收藏和回味
链接:https://pan.baidu.com/s/1FGkxkiKNmzC27mE7Pd7aLQ
提取码:v1sz
若链接失效,可在后台回复本文标题或发送邮件:Zippen-Huang@outlook.com
延伸阅读
-----------------------------------------------------------------------------
相关声明
1.如果转载本文,文末务必注明:“转自微信公众号:混沌无形”
2.若有侵权,请联系作者

全文完,感谢阅读!!如果觉得写的不错,那就点个赞或者“在看”吧。
移动机器人路径规划算法
智能移动机器人是集环境感知、动态决策、自主规划、行为控制与执行等功能为一体的机电系统。机器人自主行走是移动机器人技术的核心问题之一,其涉及到导航中的环境感知、自主定位、路径规划等关键技术。
自主导航是实现智能移动机器人自主行走与避障的关键,而路径规划是机器人自主导航的重要环节。当前移动机器人路径规划技术研究成果非常丰富,但全局路径规划算法仍存在前期搜索盲目、收敛性差、易收敛于局部最优解等问题,局部路径规划算法中存在寻路保守性高导致绕行现象、避障成功率低等问题。
为此论文针对上述问题开展相关研究,重点解决了全局路径规划中蚁群算法的前期搜索盲目性问题,局部路径规划中间隙法避障模型出现的绕行及死锁问题。
首先提出一种改进蚁群算法实现移动机器人全局路径规划。因初始信息素分布、启发信息计算和转移概率是蚁群算法的重要影响因素,为此提出基于初始障碍物搜索信息的初始信息素不均匀分布策略、基于障碍物边界大小的转移规则,并将人工势场法中的势能函数应用于启发式信息计算,实现蚁群算法改进和全局路径规划。
研究表明,改进算法能明显改善搜素盲目性,提升收敛速度,且在复杂地图环境中能够获得更短的路径。其次通过改进间隙法避障模型并融合蝙蝠-粒子群算法形成改进算法用于机器人局部路径规划。针对现有用于局部路径规划的间隙法避障模型易出现绕路及死锁等的局限,提出一种改进避障模型并融合蝙蝠-粒子群算法形成改进算法,并针对改进算法中存在的窄道问题提出了规划策略。
研究表明,将所提出的改进避障模型与蝙蝠-粒子群混合算法融合形成改进算法,能够有效解决局部规划中的绕路、死锁及窄道问题。随后对所提出的局部路径规划算法避障能力影响因素进行了分析和讨论。通过仿真实验研究了传感器检测半径、机器人移动速度两个参数对规划算法避障能力的影响规律。
研究表明,障碍物以确定性规律运动时传感器检测最佳半径值为移动障碍物最大半径的1.25倍,障碍物以随机性规律运动时传感器检测最佳半径值为移动障碍物最大半径的1.4倍,在该值下机器人能获得较高的避障成功率及相对较低的总路径长度及转弯角度。
研究还表明:若机器人移动速度是障碍物移动速度的2~3倍区间内,机器人具有稳定的高避障成功率。最后融合所提全局路径规划算法和局部路径规划算法形成混合路径规划算法,并开展了混合路径规划仿真实验。
仿真结果验证了混合路径规划算法的有效性。
关键词:机器人路径规划;蚁群算法改进;蝙蝠-粒子群混合算法;混合路径规划;
专辑:信息科技
专题:自动化技术
学科专业:机械工程(专业学位)。





提出了一种时间空间上的语言corridor
提出了一种基于优化的轨迹生成表达形式,并保证了安全和可行性。
提出了一个完善的开源的轨迹生成
架构
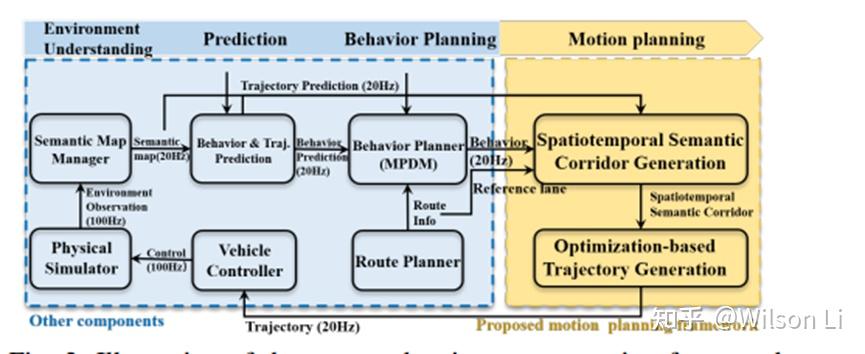
Mpdm 将决策问题表征成了一个pomdp问题,但是为了防止计算复杂度过高,将自车和其他车的状态,简单表述为有限的离散的策略例如,lane change, lane keeping。 因为mpdm提供了在不同时刻的自车的behavior,所以自车也会对不同的behavior 同时生成轨迹,这样也提高了系统的鲁棒性,例如在执行lane change的时候也会准备返回原车道的轨迹。因为决策不是本文的关键,没有详细讨论。

Corridor 是建立在frenet 坐标系下面的,因为很有物体都是和lane geometry相关的。
不同的物体被分成2类,一类是障碍物,一类是限制。
障碍物相关的物体:有具体的物理含义,在一段slt上面不允许被驶入。 例如静态物体被看成障碍物横跨了所有的时间,而动态障碍物可以被当做在不同时间上的静态障碍物。红灯也可以被看成是一个物体侵占了一段纵向距离和时间段。
限制相关的物体:表示动态限制或者时间限制。例如speed limit 和stop sign 可以被看成速度限制。Speed limit 可以被看成[s_start, s_end]上的速度限制。Lane change duration被看成在[d_start, d_end]上的时间限制。
Seed generation:
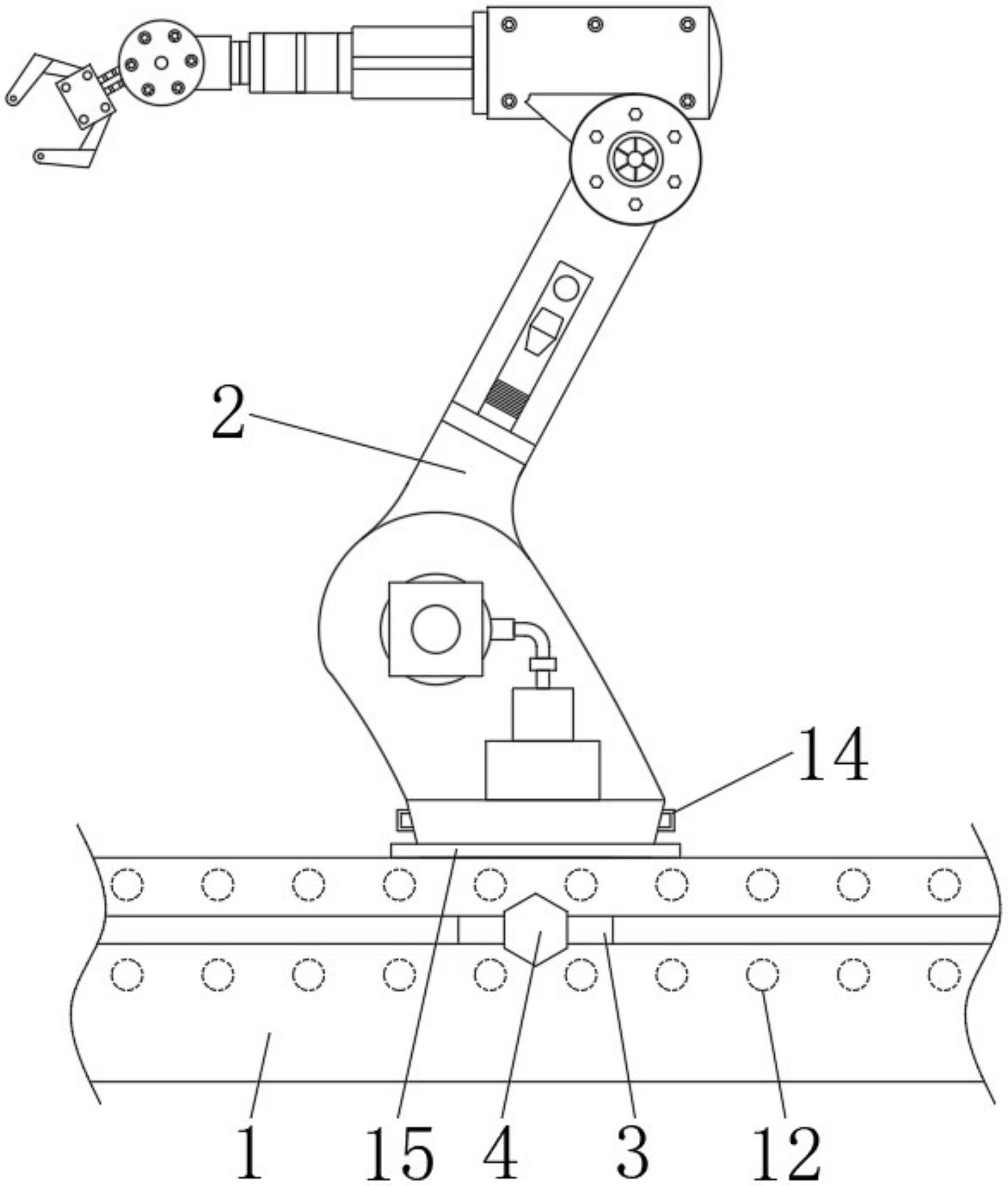
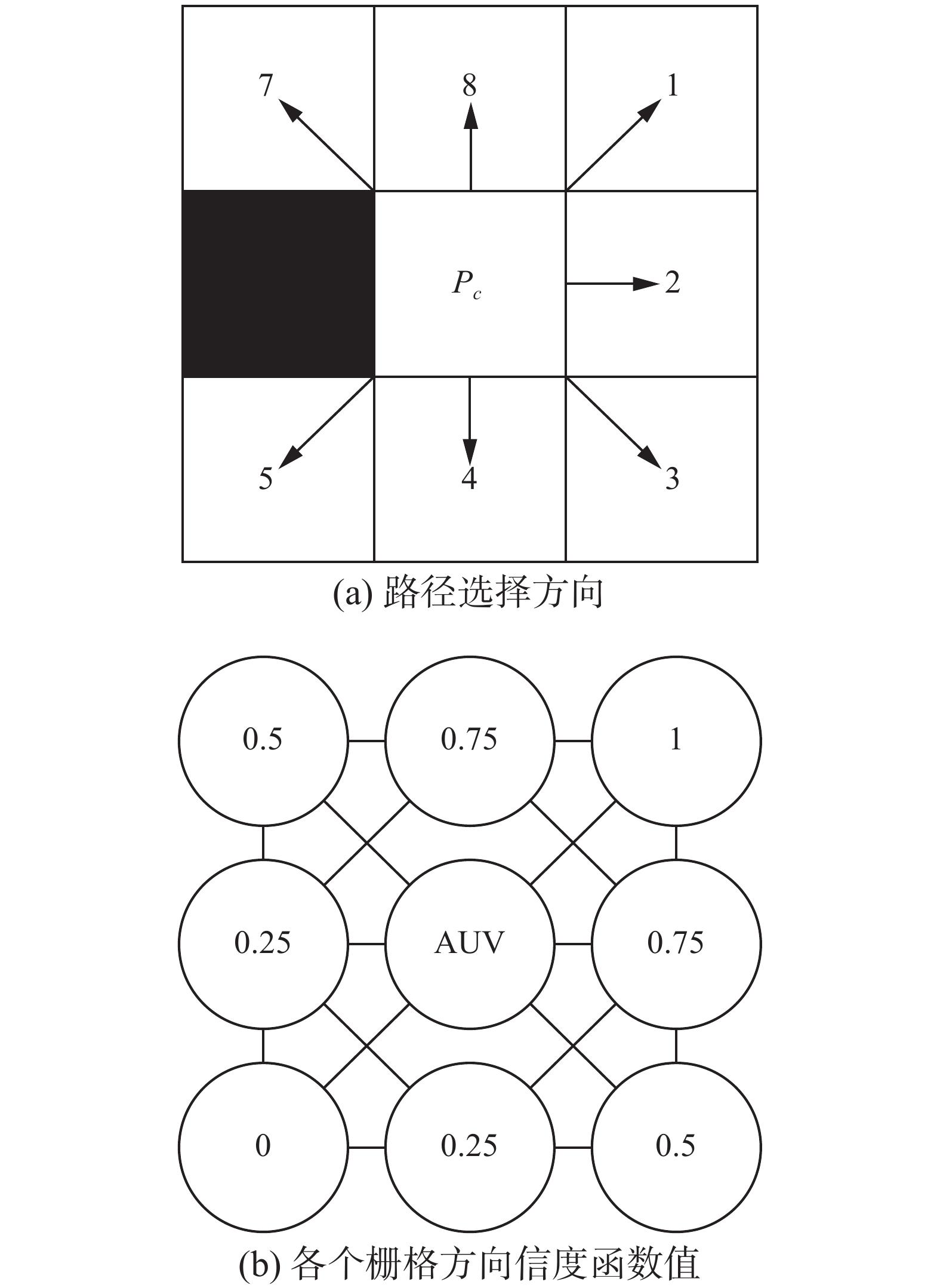
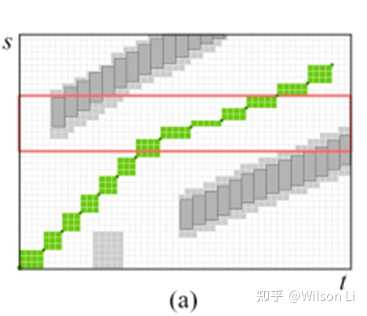
类似于图a, seed的生成是通过把behavior planning的state 映射到slt空间中形成的。保证刚刚开始的seed 是不和任何物体产生碰撞的。在seed 周边生成corridor 的目的是对free space 进行建模。
Cube inflation with boundary
类似于图b,c,通过对seed 进行slt方向轮流膨胀,直到slt方向与障碍物产生碰撞。
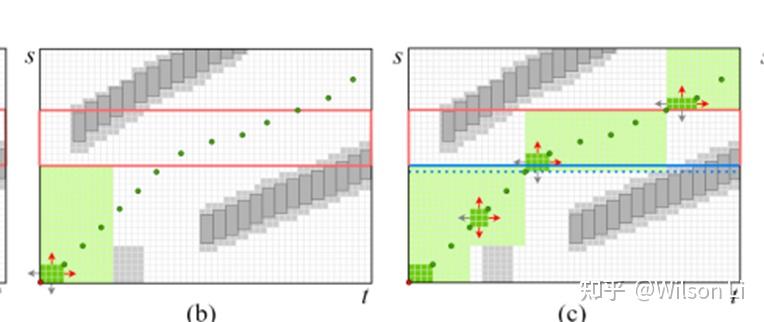
Cube relaxation
类似于图d, 通过relaxation 来松弛cube边界,同事保留硬约束。例如在纵向方法上边界通过速度限制决定s的边界,在横向上边界可以通过变道的持续时间来计算。
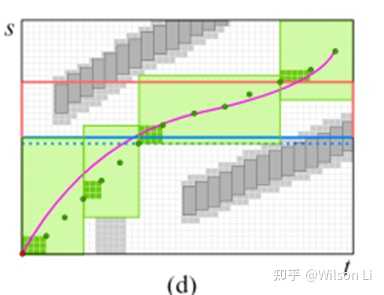
利用贝塞尔曲线


些个点事控制点。而且利用贝塞尔曲线的convex hull 性质能保证轨迹在corridor 之内。
利用分段的贝塞尔曲线来表示轨迹。分别表示s,l

Cost function 是最小化jerk ,w代表权重。

下面是经过归一化的cost
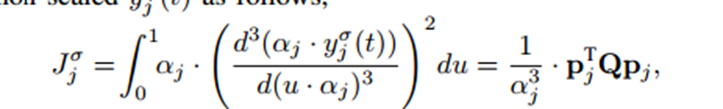
利用5次贝塞尔曲线来表示轨迹。K阶导数的表达式为:

利用convex hull 性质:
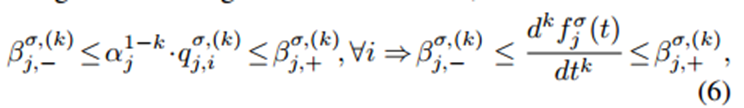
β是对于k阶导数的上下边界。
目标state约束:
同时,可以对起点和终点的状态添加0,1,2阶导数的约束。

连续性约束:

K=0,1,2,3保证jerk连续
Free space 约束:
通过把控制点给在corridor 内实现。
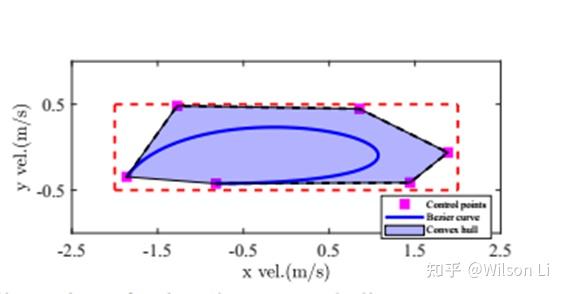
动态约束:
通过对曲线进行1,2阶求导约束,对纵向和横向的速度和加速度进行约束
当我们在做机器人或者机械臂的运动控制时,会对运动的行程距离和用时提出要求,因此要对速度和加速度进行规划,与T型速度规划相比,S型速度规划更柔和,运动过程更平稳。第一部分基于简单的模型对7段S型速度规划做理论推导,第二部分利用python进行实现。
1.1 位移、速度、加速度表达式
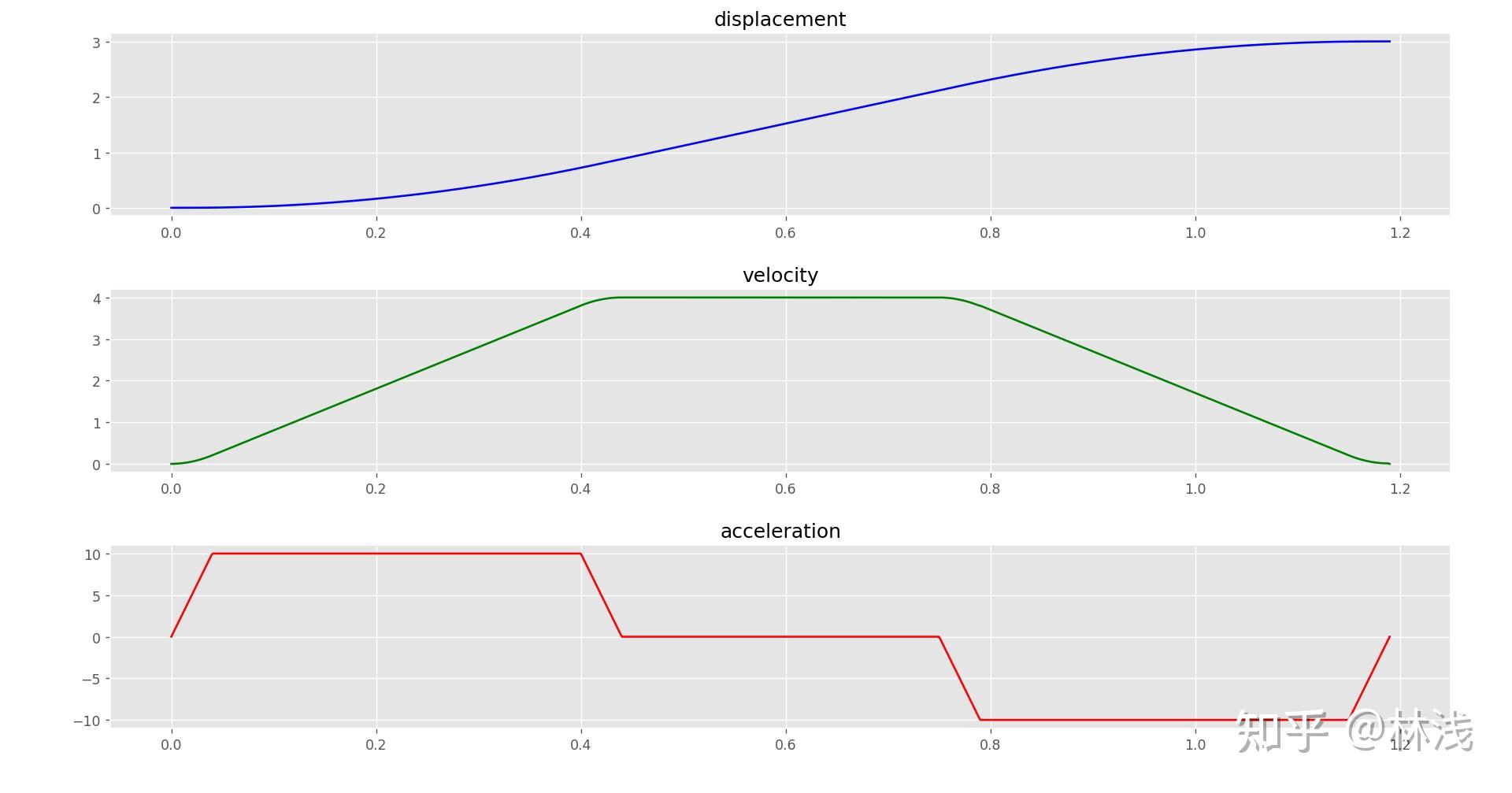
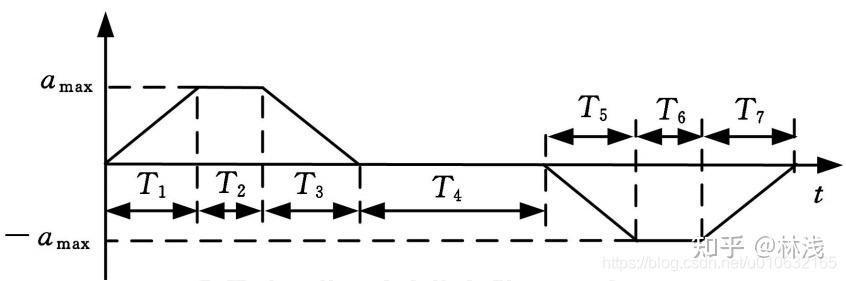
上图为典型的S型速度规划曲线,7段S型速度规划由7个过程组成,分别为:T1——加加速度运动,T2——匀加速运动,T3——减加速运动,T4——匀速运动,T5-T7与T1-T3对称,方向相反。
定义加加速度 ,为了简化运算过程,提出以下约束:
1)
2)
3) 变加速度过程 为常数
4) 初速度为0,末速度为0,起始加速度为0,结束加速度为0
因此可知加速的的表达式如下:
其中 为标量,
,
,类比匀加速运动中位移
和速度
的关系,可以推出变加速度过程中速度
与加加速度
的关系如下:
基于以上公式,可以推导出7段过程中速度的表达式为:
对于变加速度过程中位移 的公式,可以由积分得到:
因此可以推导出7段过程中位移 得表达式如下:
1.2 行程时间的表达式
在实际应用过程中,机器人或机械臂所能达到的最大加速度和速度受电机的额定转矩转速限制,而最大加加速度则由传动机构的形式所决定,因此行程距离 、峰值加速度
、峰值速度
以及加加速度
往往由外界输入,我们需要确定在这样的条件下能否满足规划的运动总时间。下面推导运动总时间
的表达式。
已知 ,再解出
和
就可以解出总行程时间
,下面进行推导。
首先,由速度 、
的表达式可知,
因此可解得
然后根据总行程 可解得
:
其中 为加速阶段的总位移,
为减速阶段的总位移,因为加速过程与减速过程完全对称,易知
,根据位移
的表达式可知:
因此可解得总行程时间 :
根据位移 和加速度
的表达式,可以利用输入的参数进行求解:
def Sacurves(Tf, J, T, N):
t_minus = Tf / N
s1=s2=s3=s4=s5=s6=0
v1=v2=v3=v4=v5=v6=0
s=np.zeros([N+1])
a=np.zeros([N+1])
amax=J*T[0]
for i in range(0, N + 1):
t=t_minus* i
if t<=T[0]:
s[i] = J* t**3/6
s1 = J* T[0] **3/6
v1 = 1/2*J*T[0]**2
a[i] = J*t
if (t>T[0]) & (t<=(T[0]+T[1])):
dt = t - T[0]
s[i] = s1+v1*dt+1/2*amax*dt**2
s2 = s1+v1*T[1]+1/2*amax*T[1]**2
v2 = v1+amax*T[1]
a[i] = amax
if (t>(T[0]+T[1])) & (t<=(T[0]+T[1]+T[2])):
dt = t - T[0] - T[1]
s[i] = s2+v2*dt+1/2*amax*dt**2-1/6*J*dt**3
s3 = s2+v2*T[2]+1/2*amax*T[2]**2-1/6*J*T[2]**3
v3 = J*T[0]*(T[0]+T[1])
a[i] = amax - J*dt
if (t > (T[0] + T[1] + T[2])) & (t <= (T[0] + T[1] + T[2] + T[3])):
dt = t - T[0] - T[1] - T[2]
s[i] = s3+v3*dt
s4 = s3+v3*T[3]
v4=v3
a[i] = 0
if (t > (T[0] + T[1] + T[2] + T[3])) & (t <= (T[0] + T[1] + T[2] + T[3] + T[4])):
dt = t - T[0] - T[1] - T[2] - T[3]
s[i] = s4+v4*dt-1/6*J*dt**3
s5 = s4+v4*T[4]-1/6*J*T[4]**3
v5 = v4 - 1/2*J*dt**2
a[i] = -1 * J * dt
if (t > (T[0] + T[1] + T[2] + T[3] + T[4])) & (t <= (T[0] + T[1] + T[2] + T[3] + T[4] + T[5])):
dt = t - T[0] - T[1] - T[2] - T[3] - T[4]
s[i] = s5+v5*dt-1/2*amax*dt**2
s6 = s5+v5*T[5]-1/2*amax*T[5]**2
v6 = v5 - amax*T[5]
a[i] = -1*amax
if (t > (T[0] + T[1] + T[2] + T[3] + T[4] + T[5])) & (t <= (T[0] + T[1] + T[2] + T[3] + T[4] + T[5] + T[6])):
dt = t - T[0] - T[1] - T[2] - T[3] - T[4] - T[5]
s[i] = s6+v6*dt-1/2*amax*dt**2+1/6*J*dt**3
a[i] = -amax + J* dt
return s,a
然后对位移进行微分求解,可得速度 的解:
def Vcurves(s, Tf, N):
t_minus=Tf / N
v=np.zeros([N+1])
for i in range(0, N):
v[i]=(s[i+1]- s[i])/t_minus
return v下面给出速度规划的总程序:
def main(amax, vmax, Sref, J, N):
# 判断是否满足七段式S曲线规划要求
T=np.zeros(7)
T[0]=amax / J
T[1]=vmax / amax - amax / J
T[2]=T[0]
T[3]=Sref / vmax - amax / J - vmax / amax
T[4]=T[0]
T[5]=T[1]
T[6]=T[0]
Tf=T.sum()
print('Tf:', Tf)
if T[1]< 0:
raise ValueError('不存在匀加速阶段')
if T[3]< 0:
raise ValueError('不存在匀速阶段')
s,a=Sacurves(Tf, J, T, N)
v=Vcurves(s, Tf, N)
t_axis=np.linspace(0, Tf, N+1)
print(s.shape, t_axis.shape)
print(s)
fig, ax=plt.subplots(3,1)
plt.tight_layout()
ax[0].plot(t_axis, s, color='b')
ax[0].set_title('displacement')
ax[1].plot(t_axis, v, color='g')
ax[1].set_title('velocity')
ax[2].plot(t_axis, a, color='r')
ax[2].set_title('acceleration')
plt.show()选取参数 进行测试,得到的结果如下:

这个专栏主要以算法为主,和大家一起手撕代码。由于理论推导和代码编写需要花费很多时间和精力,是否续更主要看大家的反馈情况。所以如果喜欢的话,点个关注不迷路,你们的点赞收藏是我更新这个专栏的最大动力~