SMO算法是干什么的？有什么作用？不要纯概念

日期：2024-04-22 14:07 / 作者：佚名

wiki:

https://en.wikipedia.org/wiki/Sequential_minimal_optimization

最近刚看完smo算法的代码，所以试着回答题主的问题。

解决svm首先将原始问题转化到对偶问题，而对偶问题则是一个凸二次规划问题，理论上你用任何一个解决凸二次规划的软件包都可以解决，但是这样通常来说很慢，大数据情况下尤其不实际，smo是微软研究院的大神发明的解决svm对偶问题的优化算法，可以更快找到好的解。通常而言分简化版和优化版smo算法。

简化版:每次迭代随机选取alpha_i和alpha_j,当然其中要有一个违反kkt条件，通常先选一个违反kkt条件的alpha_i，然后随机选择一个alpha_j,然后用类似坐标上升(下降)的算法来优化目标函数，具体细节题主可以看相关代码，推荐《machine learning in action》的svm部分，但是这样的优化方式并不是最快的；

优化版:用启发式的算法选择alpha_j,即选择alpha_j,使得|Ei-Ej|最大，至于为什么，因为变量的更新步长正比于|Ei-Ej|,也就是说我们希望变量更新速度更快，其余的和简化版其实区别不大；

应该还有其他版本的smo，没看过不做评论，希望对题主有用。

SMO(Sequential Minimal Optimization)是针对求解SVM问题的Lagrange对偶问题，一个二次规划式，开发的高效算法。传统的二次规划算法的计算开销正比于训练集的规模，而SMO基于问题本身的特性（KKT条件约束）对这个特殊的二次规划问题的求解过程进行优化。对偶问题中我们最后求解的变量只有Lagrange乘子 ${\\vec \\alpha }$ 向量，这个算法的基本思想就是每次都只选取一对 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$ ，固定 ${\\vec \\alpha }$ 向量其他维度的元素的值，然后进行优化，直至收敛。

SMO干了什么？

首先，整个对偶问题的二次规划表达如下：

$\\begin{align} \\mathop{\\max }\\limits_{\\vec \\alpha }& \\quad \\sum\\limits_{i=1}^n{{\\alpha _i}}- \\frac{1}{2}\\sum\\limits_{i=1}^n{\\sum\\limits_{j=1}^n{{\\alpha _i}{\\alpha _j}{y_i}{y_j}{\\bf{x}}_i^T{{\\bf{x}}_j}}}\\\\ s.t.& \\quad \\sum\\limits_{i=1}^n{{\\alpha _i}{y_i}}=0 \\\\ & \\quad{\\alpha _i}\\ge 0, \\quad i=1,2, \\ldots ,n \\end{align}$

SMO在整个二次规划的过程中也没干别的，总共干了两件事：

选取一对参数 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$
固定 ${\\vec \\alpha }$ 向量的其他参数，将 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$ 代入上述表达式进行求最优解获得更新后的 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$

SMO不断执行这两个步骤直至收敛。

因为有约束 $\\sum\\limits_{i=1}^n{{\\alpha _i}{y_i}}=0$ 存在，实际上 $\\[{{\\alpha _i}}\\]$ 和 $\\[{{\\alpha _j}}\\]$ 的关系也可以确定。 ${\\alpha _i}{y_i}+{\\alpha _j}{y_j}=C$ 这两个参数的和或者差是一个常数。

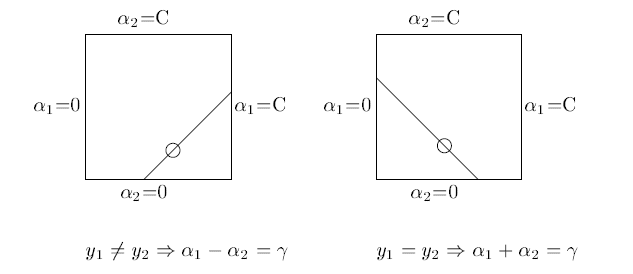
所以虽然宣传上说是选择了一对 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$ ，但还是选择了其中一个，将另一个写作关于它的表达式代入目标函数求解。

为什么SMO跑的那么快，比提出之前的算法不知道高到哪里去了？

正如上面提到的，在固定其他参数以后，这就是一个单变量二次规划问题，仅有的约束也是这个变量 $\\alpha _i \\ge 0$ ，显然有闭式解。不必再调用数值优化算法。

KKT条件是对偶问题最优解的必要条件：

$\\begin{cases} {{\\alpha _i}\\ge 0}\\\\ {{y_i}f\\left({{{\\bf{x}}_i}}\\right) - 1 \\ge 0}\\\\ {{\\alpha _i}\\left({{y_i}f\\left({{{\\bf{x}}_i}}\\right) - 1}\\right)=0} \\end{cases}$

除了第一个非负约束以外，其他约束都是根据目标函数推导得到的最优解必须满足的条件，如果违背了这些条件，那得到的解必然不是最优的，目标函数的值会减小。

所以在SMO迭代的两个步骤中，只要 $\\left({{\\alpha _i},{\\alpha _j}}\\right)$ 中有一个违背了KKT条件，这一轮迭代完成后，目标函数的值必然会增大。Generally speaking，KKT条件违背的程度越大，迭代后的优化效果越明显，增幅越大。

怎样跑的更快？

和梯度下降类似，我们要找到使之优化程度最大的方向（变量）进行优化。所以SMO先选取违背KKT条件程度最大的变量，那么第二个变量应该选择使目标函数值增大最快的变量，但是这个变量怎么找呢？比较各变量优化后对应的目标函数值的变化幅度？这个样子是不行的，复杂度太高了。

SMO使用了一个启发式的方法，当确定了第一个变量后，选择使两个变量对应样本之间最大的变量作为第二个变量。直观来说，更新两个差别很大的变量，比起相似的变量，会带给目标函数更大的变化。间隔的定义也可以借用偏差函数

$\\[{E_i}=\\max \\left({{y_i}f\\left({{{\\bf{x}}_i}}\\right) - 1,0}\\right)\\]$

我们要找的也就是使对于 $\\alpha_i$ 来说使 $\\left|{{E_i}-{E_j}}\\right|$ 最大的 $\\alpha_j$

很惭愧，只做了一点微小的工作。

References

[1]Platt, John. "Sequential minimal optimization: A fast algorithm for training support vector machines." (1998).

是用来求解出SVM的带约束的优化问题的对偶问题的最优解的二次规划方法，通过求解出对偶问题的最优解，从而得到原始问题的最优解。

这种方法通过不断地将对偶问题的二次规划问题分解成为只有两个变量的二次规划问题，并对子问题求解，通过不断地更新，迭代找出所有约束变量值。

SMO算法的具体步骤如下：

1.确定非线性支持向量机的优化目标：

$min \\frac{1}{2}\\sum_{i=1}^{m}{\\sum_{j=1}^{m}{\\alpha_{i}\\alpha_{j}y^{i}y^{j}K(X^{i}.X^{j})-\\sum_{i=1}^{m}{\\alpha_{i}}}}$

$s.t. \\sum_{i=1}^{m}{\\alpha_{i}y^{i}}=0$

$0\\le \\alpha_{i}\\leq C$

2.选择出两个变量 $\\alpha_{1}，\\alpha_{2}$ ，将优化问题转化成

$min \\frac{1}{2}K_{11}\\alpha_{1}^{2}+\\frac{1}{2}K_{22}\\alpha_{2}^{2}+y^{(1)}y^{(2)}K_{12}\\alpha_{1}\\alpha_{2}-(\\alpha_{1}+\\alpha_{2})+y^{(1)}\\alpha_{1}\\sum_{k=3}^{m}{y^{(k)}\\alpha_{k}K_{k1}}+y^{(2)}\\alpha_{2}\\sum_{k=3}^{m}{y^{(k)}\\alpha_{k}K_{k2}}+M_{1}$

$s.t. \\alpha_{1}y^{1}+\\alpha_{2}y^{2}=-\\sum_{k=3}^{m}{\\alpha_{k}y^{(k)}}=M_{2}$

$0\\le \\alpha_{i}\\leq C$

3.将上面不等式约束变成只对 $\\alpha_{2}$ 求解的最优化问题。

求解出的 $\\alpha_{2}^{(i+1)}=H$ $\\alpha_{2}^{(i+1)}>H$

$\\alpha_{2}^{(i+1)}=\\alpha_{2}^{(i+1)}$ $L\\leq \\alpha_{2}^{(i+1)}\\leq H$

$\\alpha_{2}^{(i+1)}=L$ $\\alpha_{2}^{(i+1)}<L$

$\\alpha_{1}^{(i+1)}=\\alpha_{1}^{(i)}+y^{(1)}y^{(2)}(\\alpha_{2}^{(i)}-\\alpha_{2}^{(i+1)})$

更新完 $\\alpha_{1}和\\alpha_{2}$ 重新计算阈值b与误差 $E_{i}$

输入公式实在太麻烦了。等我有心情了，再把公式补上。

SMO 算法是用来给 SVM 求解的。因此，想要理解 SMO，就必须先理解 SVM 的目标函数式。下面我讲的是软间隔支持向量机，硬间隔支持向量机可以通过把 $C$ 设置为无穷大来得到。

为了避免讲一大堆与 SMO 不相关的内容，我假设读者已经知道 SVM 原问题的对偶问题：

$\\min_\\alpha \\sum_{i=1}^n\\sum_{j=1}^n\\alpha_i\\alpha_jy_iy_j(x_i\\cdot x_j)-\\sum_{i=1}^n\\alpha_i \\\\ \\begin{aligned}s.t. \\ \\sum_{i=1}^n\\alpha_iy_i=0 \\\\ 0\\leq \\alpha_i\\leq C \\end{aligned}$

上述目标函数在约束条件下得到最优解，充分必要条件是找到一组满足 KKT 条件的参数 $\\alpha$ 。此问题的 KKT 条件可以分为四个部分。

第一个部分是对拉格朗日函数求导得到的等式约束：

$w=\\sum_{i=1}^N\\alpha_iy_ix_i \\\\ C=\\alpha_i+\\mu_i \\\\ \\sum_{i=1}^N\\alpha_iy_i=0$

第二个部分是对偶互补条件，这是 SMO 算法推导的关键：

$\\alpha_i(y_i(w\\cdot x_i+b)-1+\\xi_i)=0 \\\\ \\mu_i\\xi_i=0 \\\\$

第三部分是原问题的不等式约束：

$y_i(w\\cdot x_i+b)-1+\\xi_i\\geq0 \\\\ \\xi_i\\geq0$

第四部分是拉格朗日乘子的约束：

$\\alpha_i\\geq0 \\\\ \\mu_i\\geq0$

由 $C=\\alpha_i+\\mu_i$ 与第四部分的约束可以得到下面的约束，这也是对偶问题约束的来源：

$0\\leq\\alpha_i\\leq C \\\\$

以上是 SVM 的目标函数，下面开始讲 SMO。

SMO 算法在在迭代过程中始终保持所有的等式约束成立。同时 SMO 也保持不等式约束 $0\\leq \\alpha_i\\leq C$ 成立（注意，在等式 $C=\\alpha_i+\\mu_i$ 成立的前提下， $0\\leq \\alpha_i\\leq C$ 成立也就意味着 $\\mu_i\\geq0$ 成立）。也就是说，SMO 算法在 $[0,C]$ 区间内调整 $\\alpha_i$ 。初始时 SMO 设置所有的 $\\alpha_i=0$ 。注意，此时的参数是不满足 KKT 条件的约束的。

我们知道，KKT 条件被满足是原问题与对偶问题得到最优解的充分必要条件。因此最优化的目标就是将 $\\alpha_i$ 调整到 KKT 条件被满足的状态。

那么，什么样的参数满足 KKT 条件约束呢？我们从 KKT 条件本身出发来分析一下：

我们知道 $0\\leq \\alpha_i\\leq C$ ，因此可以将 $\\alpha_i$ 分为三种情况来分析：

第一种情况， $\\alpha_i=C$ 时：

由 $\\alpha_i(y_i(w\\cdot x_i+b)-1+\\xi_i)=0$ 知道 $y_i(w\\cdot x_i+b)-1+\\xi_i=0$
由 $C=\\alpha_i+\\mu_i$ 知道 $\\mu_i=0$ ，此时 $\\mu_i\\xi_i=0$ 对 $\\xi_i$ 无约束， $\\xi_i$ 可以是任何大于等于 0 的值。
$y_i(w\\cdot x_i+b)-1+\\xi_i=0$ 与 $\\xi_i\\geq0$ 综合起来，我们知道 $y_i(w\\cdot x_i+b)\\leq1$ 。
这个结论可以从 SVM 的设计上理解： $\\xi_i$ 是样本 $x_i$ 的松弛量，只有当 $x_i$ 被错误分类时，才有 $\\xi_i>0$ ，而 $x_i$ 被错误分类即对应着 $y_i(w\\cdot x_i+b)<1$ 。

第二种情况， $\\alpha_i=0$ 时：

由 $C=\\alpha_i+\\mu_i$ 知道 $\\mu_i=C$ ，此时由 $\\mu_i\\xi_i=0$ 有 $\\xi_i=0$ 。
由 $y_i(w\\cdot x_i+b)-1+\\xi_i\\geq0$ 可知 $y_i(w\\cdot x_i+b)\\geq1$ 。
这个结论也可以从 SVM 的设计上理解： $\\xi_i$ 是样本 $x_i$ 的松弛量， $\\xi_i=0$ 时， $x_i$ 必须被正确分类，即 $y_i(w\\cdot x_i+b)\\geq1$ 。

第三种情况， $0<\\alpha_i< C$ 时：

由 $C=\\alpha_i+\\mu_i$ 知道 $\\mu_i=C-\\alpha_i\ eq0$ ，此时由 $\\mu_i\\xi_i=0$ 有 $\\xi_i=0$ 。
由 $\\alpha_i(y_i(w\\cdot x_i+b)-1+\\xi_i)=0$ 有 $y_i(w\\cdot x_i+b)=1$ 。
由 SVM 的性质可以知道，当 $y_i(w\\cdot x_i+b)=1$ 时， $x_i$ 是支持向量。

可以看到，对于我们的优化来说， $\\mu_i$ 和 $\\xi_i$ 本身的值并不重要，对于任意一种 $\\alpha_i$ 的情况，只要对应的 $y_i(w\\cdot x_i+b)$ 的条件满足，就一定有合法的 $\\mu_i$ 与 $\\xi_i$ 能让我们取到。

所以现在情况很清楚了，对于每一个 $\\alpha_i$ ，如果：

$\\alpha_i=C$ ，那么 $x_i$ 必须被错误分类或者是支持向量，必须有 $y_i(w\\cdot x_i+b)\\leq1$ 。
$0<\\alpha_i< C$ ，那么 $x_i$ 必须是支持向量，必须有 $y_i(w\\cdot x_i+b)=1$ 。
$\\alpha_i=0$ ，那么 $x_i$ 必须被正确分类，必须有 $y_i(w\\cdot x_i+b)\\geq1$ 。

当上面这三条约束对所有的 $i$ 都成立时，KKT 条件就满足了，我们就得到了最优解。因此我们做 SVM 最优化，目标就是在保持所有等式约束的前提下，使得所有的样本点满足上述条件。

由于不同的 $\\alpha$ 之间相互制约，一次性将所有的 $\\alpha$ 优化到满足 KKT 条件是一个比较难的问题。因此 SMO 算法采用迭代的方法进行优化。

具体地，SMO 每次选择一个违反了 KKT 条件的 $\\alpha_i$ ，也就是说，如果：

$\\alpha_i=C$ ，且 $y_i(w\\cdot x_i+b)>1$ ；
$0<\\alpha_i< C$ ，且 $y_i(w\\cdot x_i+b)\ eq1$ ；
$\\alpha_i=0$ ，且 $y_i(w\\cdot x_i+b)<1$ 。

那么 SMO 在本轮迭代就可以优化 $\\alpha_i$ ，怎么优化呢？我们再回头来看一下我们的最小化目标：

这里首先要理解的是，KKT 约束与上面的最小化目标是一致的，因为上述最优化目标取到最小值的充分必要条件是 KKT 条件被满足。我们刚才把最小化目标函数的目标转化为满足 KKT 条件的约束，因为满足 KKT 条件约束就能最小化目标函数；而现在我们要再将目标转化回来：我们可以通过直接最小化目标函数，使得 KKT 条件约束更完全地被满足。

所以我们现在的任务，就是通过调整 $\\alpha_i$ 来直接最小化这个目标函数。其余的 $\\alpha_j$ 全都固定时，上面的这个最优化问题其实就是对于 $\\alpha_i$ 的一个简单的一元函数优化问题。

不过等等，我们突然注意到约束 $\\sum_{i=1}^n\\alpha_iy_i=0$ 。这个约束中的任何一个 $\\alpha_i$ 单独更改，都会使得约束不满足。因此，只挑选一个 $\\alpha_i$ 是不够的，我们还需要挑选另一个 $\\alpha_j$ 与 $\\alpha_i$ 同步变化，使得 $\\alpha_i$ 有调整的余地。 $\\alpha_j$ 的选择比较随意，只要能够使得目标函数下降即可。

我们把除 $\\alpha_i$ 与 $\\alpha_j$ 之外的所有变量隐去，可以得到目标

$\\min_{\\alpha_i,\\alpha_j}\\alpha_i\\alpha_jy_iy_j(x_i\\cdot x_j)+\\alpha_i\\alpha_iy_iy_i(x_i\\cdot x_i)+\\alpha_j\\alpha_jy_jy_j(x_j\\cdot x_j)-\\alpha_i-\\alpha_j \\\\ \\begin{aligned}s.t. \\ \\alpha_iy_i+\\alpha_jy_j+\\zeta=0 \\\\ 0\\leq \\alpha_i\\leq C\\\\ 0\\leq \\alpha_j\\leq C \\end{aligned}$

其中 $\\zeta$ 就是所有其他固定的 $\\alpha y$ 的和。

接下来，只需要按照 $\\alpha_iy_i+\\alpha_jy_j+\\zeta=0$ 得到 $\\alpha_i=-\\frac{\\alpha_jy_j+\\zeta}{y_i}$ ，回代到目标函数中，得到新的目标函数，这个函数太复杂了，我懒得算了...反正可以想得到它是 $\\alpha_j$ 的二次函数，可以直接对 $\\alpha_j$ 求导得到最优解。

当然，得出来的最优解不一定符合这个约束

$0\\leq-\\frac{\\alpha_jy_j+\\zeta}{y_i}\\leq C\\\\ 0\\leq \\alpha_j\\leq C$

我们接下来只需要选择约束区间内，最接近最优解的那个值就好了（因为二次函数一定是对称的，最越接近最小值的点，二次函数的值越小）。

这就是一步迭代中，我们做的事情。接下来要做的，就是反复迭代选出违反 KKT 约束的量，然后进行这样的优化，直到不再有违反 KKT 条件约束的量，我们就得到了最优解。

SMO 还有一个启发式的优化技巧。就是在 $\\alpha_i$ 与 $\\alpha_j$ 的选择过程中，我们可以选择更好的 $\\alpha_i$ 与 $\\alpha_j$ ，使得目标函数值尽可能多地下降。

在选择 $\\alpha_i$ 时，我们选择违反 KKT 条件最严重的样本点 $\\alpha_i$ 。

在选择 $\\alpha_j$ 时，我们选择能够使得优化后的目标函数值最小的 $\\alpha_j$ 。也就是说，我们可以挨个试一下所有的 $\\alpha_j,j\ eq i$ ，分别计算按照这些 $\\alpha_j$ 与 $\\alpha_i$ 迭代一步后的目标函数值。然后我们选择结果最小的那个，作为我们最终的选择。