

首先非常感谢 @远去的飞鹰 对上一期算法中存在的问题进行更正:

现已将“最个体”改正为“最优个体”。哈里斯鹰算法(Harris Hawks Optimizer,HHO)是由Heidari、Mirjalili等人于2019年提出的一种元启发式算法,不得不说Mirjalili教授是真滴厉害!哈里斯之鹰主要生活在美国亚利桑那州南部地区,其之所以与众不同,是因为它会与群体中的其他家庭成员一起进行独特的合作觅食活动,而其他种类的猛禽则通常独自捕食猎物。正因如此,哈里斯鹰独特的群体捕食行为才非常适合被模拟成一种群智能优化过程。

1.全局搜索阶段
在自然界中,哈里斯鹰会利用其犀利的双眼侦查环境、追踪猎物。但是,在茫茫的亚利桑那州南部地区,有时候日子并不好过。在沙漠地区,其常常需要花费几个小时来等待,观察,并追踪猎物。因此,哈里斯鹰的群体内部分散度很高,其个体随机栖息在某些位置,并根据两种策略探测猎物:
a.当q <0.5时,哈里斯鹰会根据其它成员和猎物的位置进行栖息;
b.当q ≥0.5时,哈里斯鹰会随机栖息在种群活动范围内的某颗树上。
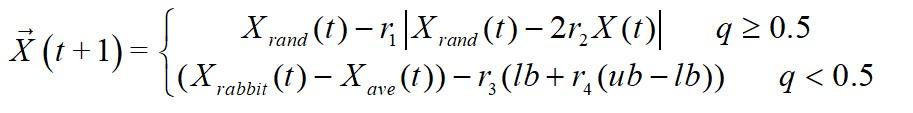
其中q、r1、r2、r3、r4均为[0,1]内的随机数,ub、lb为搜索空间上、下限;Xrand 为一随机个体位置;Xrabbit 为猎物位置,Xave为种群内所有个体的平均位置。r3是一个比例系数,一旦r4的值接近1,就会进一步增加该策略的随机性。类似于鲸鱼优化算法,绝对值中的内容可看作两个体间的相对距离;r1为随机的比例系数,其为哈里斯鹰的栖息提供多样化趋势并使其能够探索不同区域的特征空间。
2.由全局搜索阶段转换至局部开发阶段
哈里斯鹰可以根据猎物的逃逸能量来进行不同状态的转换。在猎物的逃脱过程中,其逃逸能量E 将大大降低:
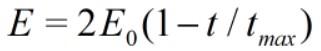
鉴于不同猎物间的逃逸能量存在差异,故原文令E0(逃逸能量初始值)在算法迭代过程中于[-1,1]内随机变化。关于这个逃逸能量初始值,原文给了这样的解释:
“When the value of E0 decreases from 0 to -1, the rabbit is physically flagging, whilst when the value of E0 increases from 0 to 1, it means that the rabbit is strengthening. The dynamic escaping energy E has a decreasing trend during the iterations.”
当E0由0减小至-1时(E0<0),此时兔兔“身体越加疲乏”?其实可以理解为兔兔不断逃跑耗费了很多能量,所以越来越虚;当E0由0增加至1时(E0>0),兔兔处于恢复能量阶段。当|E |≥1时,哈里斯鹰搜索不同的区域以进一步探索猎物的位置,此时对应全局搜索阶段;当|E |<1时,哈里斯鹰对相邻的解进行局部勘探,故而对应局部开发阶段。不知道为什么,写这篇文章时我总是会想到这个表情包:

原文给出了500次迭代条件下E 的两条迭代曲线:
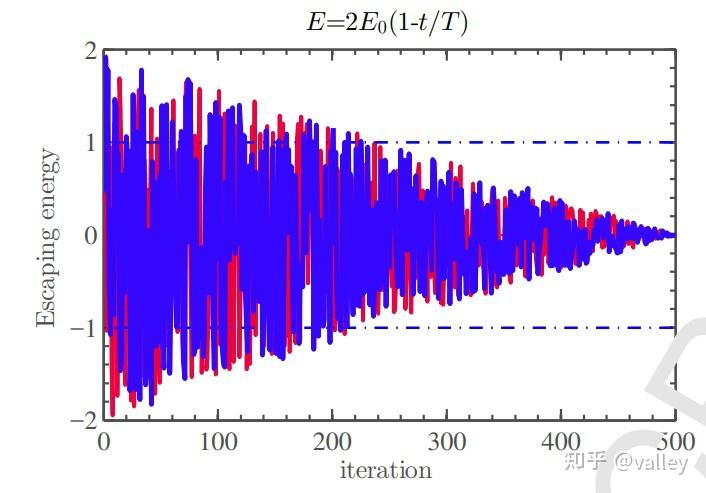
3.局部开发阶段
在此阶段中,哈里斯鹰开始对猎物进行突袭。不幸的是,猎物经常先哈里斯鹰一步逃脱。因此,根据猎物的逃逸行为和自身的追逐策略,哈里斯鹰演变出了四种攻击策略。
在说四种策略之前,要先提一下攻击的前提。假设r 为兔兔逃脱概率,r <0.5时为成功逃脱,相反r ≥0.5为逃脱失败。通常情况下,哈里斯鹰会以强硬或轻柔的围攻方式来捕获猎物(一柔一刚,不得不佩服作者的想象力)。这围攻方式意味着哈里斯鹰将根据猎物的剩余能量从不同方向轻柔或强硬地攻击猎物。在实际情况下,哈里斯鹰会越来越接近预期的猎物,并通过突袭而增加了合作杀死猎物的机会。一段时间后,猎物将损失越来越多的能量,这时哈里斯鹰便加强围攻过程,从而捕获猎物。在这个过程中,逃逸能量E 的作用不言而喻。原文假设|E |≥0.5时,进行轻柔围攻;当|E |<0.5时,进行强硬围攻。
3.1轻柔围攻
当r ≥0.5且|E |≥0.5时,兔兔仍然有足够的能量,此时哈里斯鹰若是霸王硬上弓则势必得不偿失。因此,哈里斯鹰在兔兔身边不断徘徊,磨其心智,使其疲惫,进而突袭:
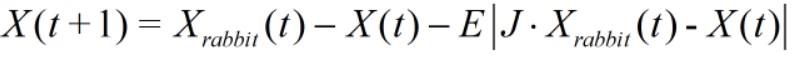
其中J 为兔兔逃跑过程中的跳跃距离,J=2*(1-rand)。
3.2强硬围攻
当r ≥0.5且|E |<0.5时,兔兔非常疲惫,面对强敌唯以头抢地尔。此时哈里斯鹰直接霸王硬上弓:
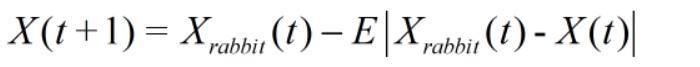
图3为该攻击模式的模拟图:
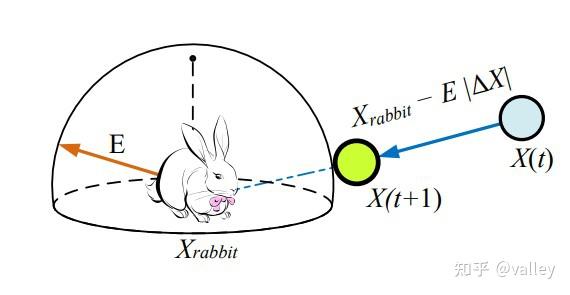
3.3渐进式快速俯冲的轻柔围攻
当r <0.5且|E |>0.5时,兔兔有机会逃脱,且逃逸能量足够。针对这种情况,哈里斯鹰需要在进攻前形成一个渐进式快速俯冲的轻柔围攻方式,具体通过以下策略实施:
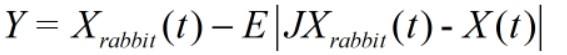
此番更新后,若是适应度值没有改善,则执行另一种策略:
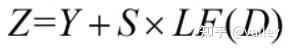
其中D 为空间维度,S 是一个1×D 的随机向量,即S=randn(1,D);LF (D)为Levy飞行函数:
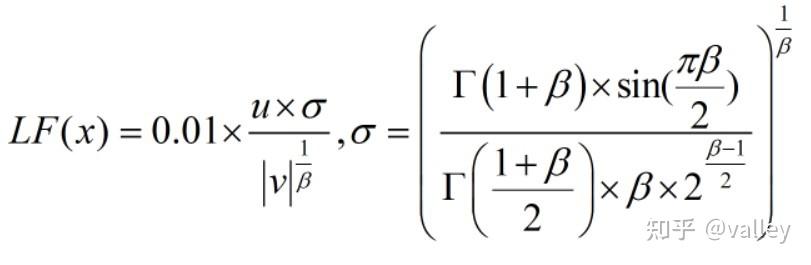
其中u、v 为[0,1]内均匀分布的随机数, β=1.5。综上所述,该围攻方式可总结为:
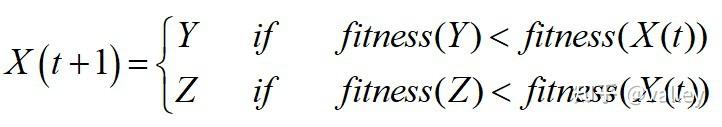
由此可得渐进式快速俯冲的轻柔围攻总体矢量示例图:
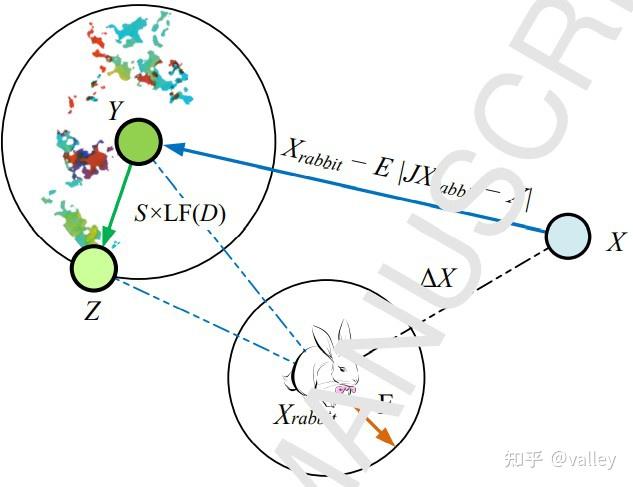
3.4渐进式快速俯冲的强硬包围
当r<0.5且|E |<0.5时,兔兔有机会逃逸,但逃逸能量不足,因此哈里斯鹰在突袭前先形成一个强硬包围圈,稳住场面,再缩小它们和猎物的平均距离。我认为之所以设置这样一种情况是因为如果强攻,则搜索半径迅速缩小,这反而帮助猎物节省能量从而趁机逃脱。不得不说哈里斯鹰老司机啊,就是到手的肉也要保证万无一失:
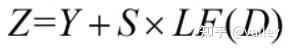
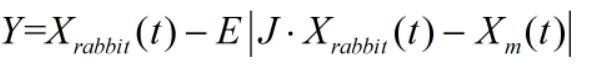
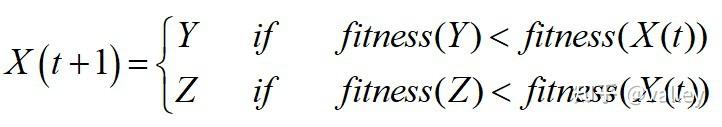
由此可得渐进式快速俯冲的强硬围攻总体矢量示例图:
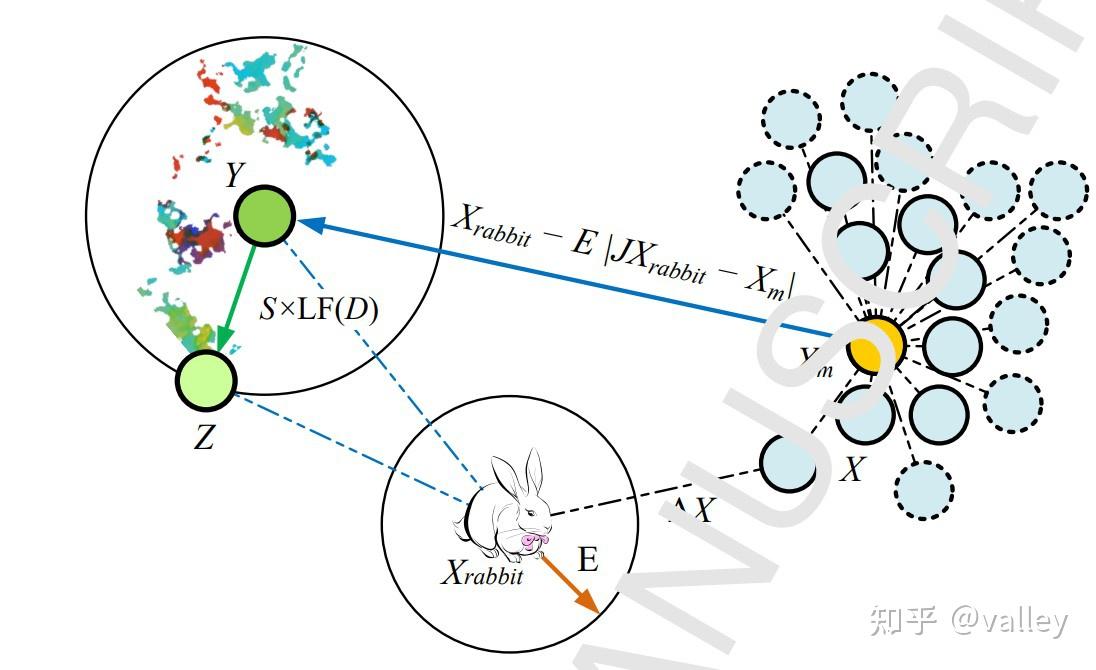
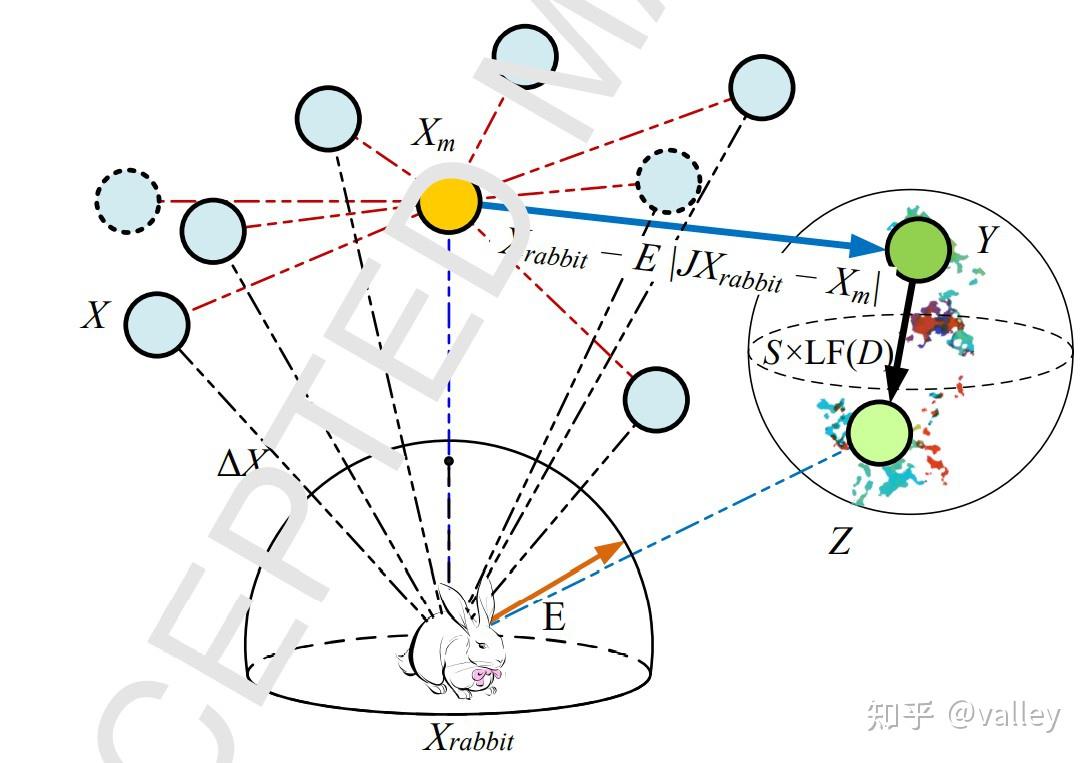
综上所述,HHO算法的捕食策略简图及迭代伪代码为:
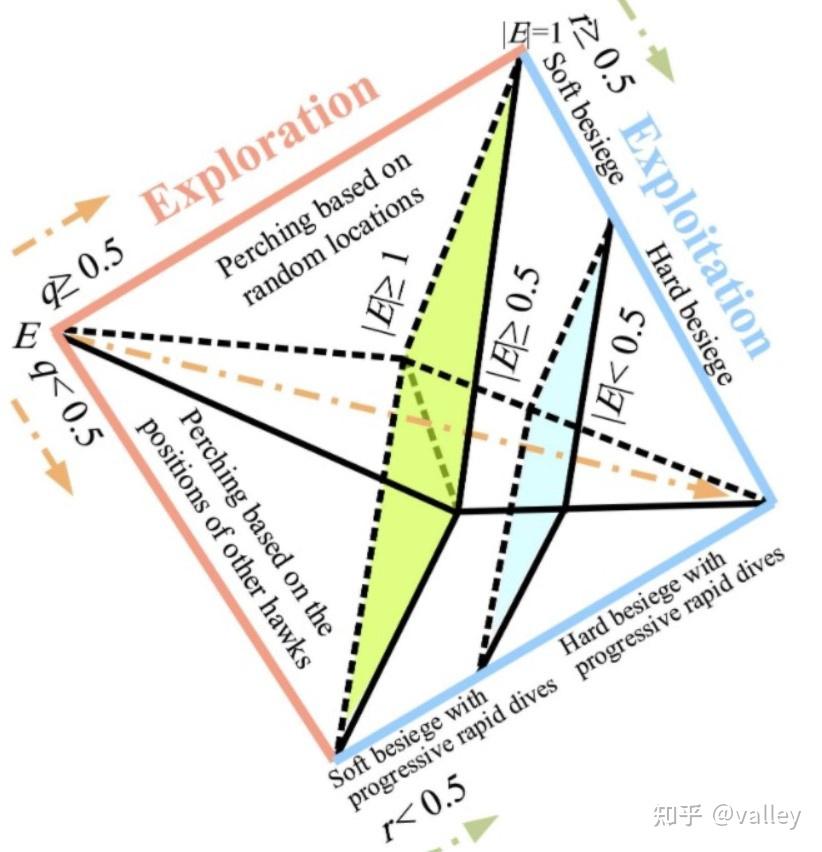

最近逛Mathwork时发现了有趣的桁架优化设计问题,这个模型简直就和理论力学中学的一模一样!只不过理论力学求的是受力,而非重量优化。本次测试就对他开刀。
10杆桁架优化设计问题
该问题的主要目的是最大化的降低结构的整体重量。在计算中对许用应力和节点位移限值的各种组合的横截面积使用离散值和连续值。图8显示了10根悬臂桁架的几何形状、支撑和负载条件:
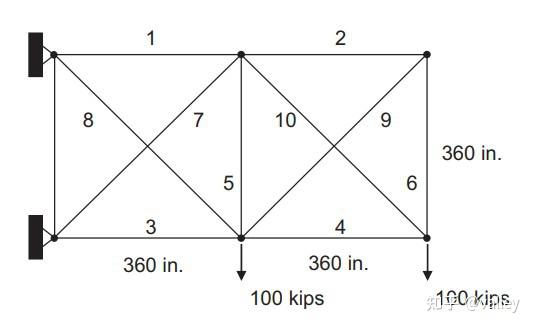
桁架构件的最大容许应力为±25千磅力/平方英寸,垂直和水平方向上的最大节点挠度为±2.0in。该材料的单位重量为0.1磅/立方英寸,弹性模量为10^7磅/平方英寸。注意有如下转换:
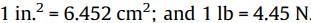
离散变量状态
顾名思义,该状态下的参数由一组41个离散值构成:(1.62, 1.80, 1.99, 2.13, 2.38, 2.62, 2.88, 2.93, 3.09, 3.13, 3.38, 3.47, 3.55, 3.63, 3.84, 3.87, 3.88, 4.18, 4.22, 4.49, 4.59, 4.80, 4.97, 5.12, 5.74, 7.22, 7.97, 11.5, 13.5, 13.9, 14.2, 15.5, 16.0, 16.9, 18.8, 19.9, 22.0, 22.9, 26.5, 30.0, and 33.5 )。这就有点像穷举法,只是组合的问题,所以不太想做。原文给出了几种对比结果:
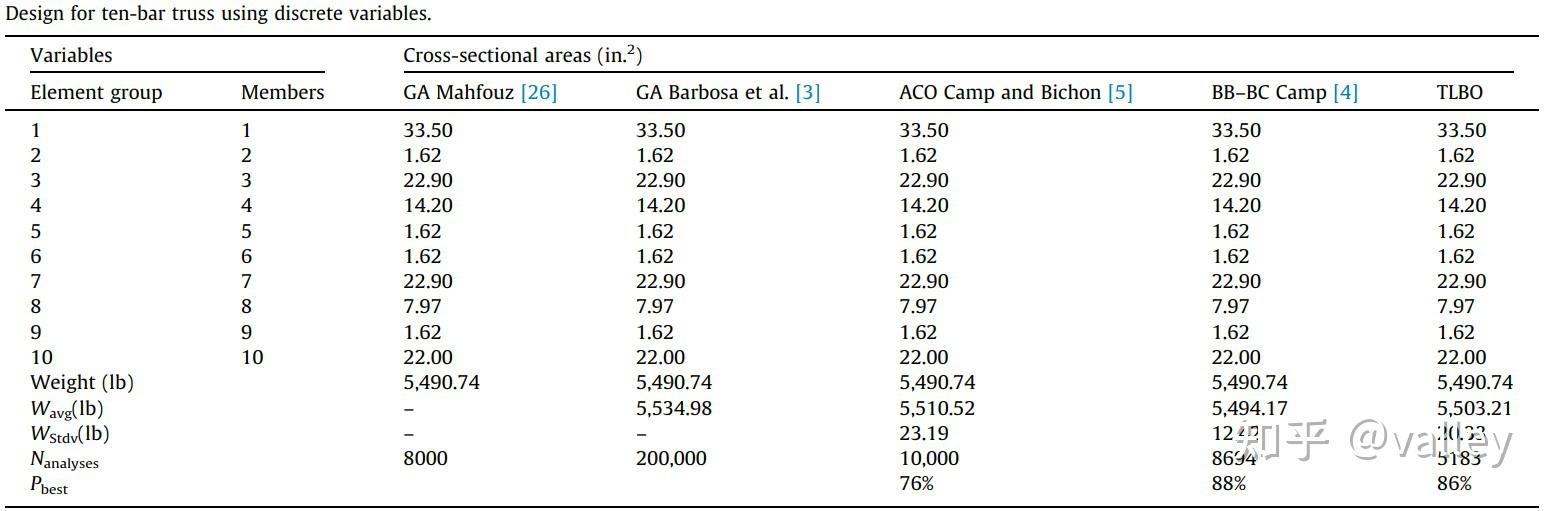
可以看出每种算法所得参数组合均相同,只不过成功率存在差异而已。
连续变量状态
该状态下每根杆的横截面积均处于[0.1,35]平方英寸内,因此非常适合用算法去优化。本次测试选取GWO与HHO进行对比,种群规模设为30,最大迭代次数为500,运算10次后取参数平均值。下图9为某次三种算法的迭代曲线:
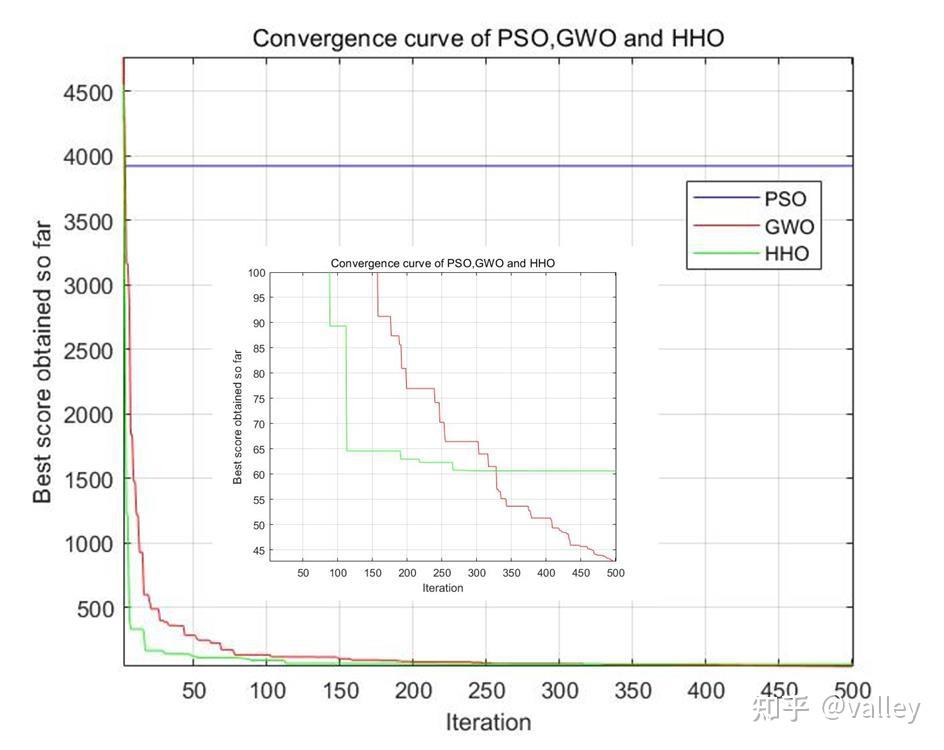
为了更贴合原文数据,将种群规模改为10,最大迭代次数改为100,下图10为修改后三种算法的迭代曲线:
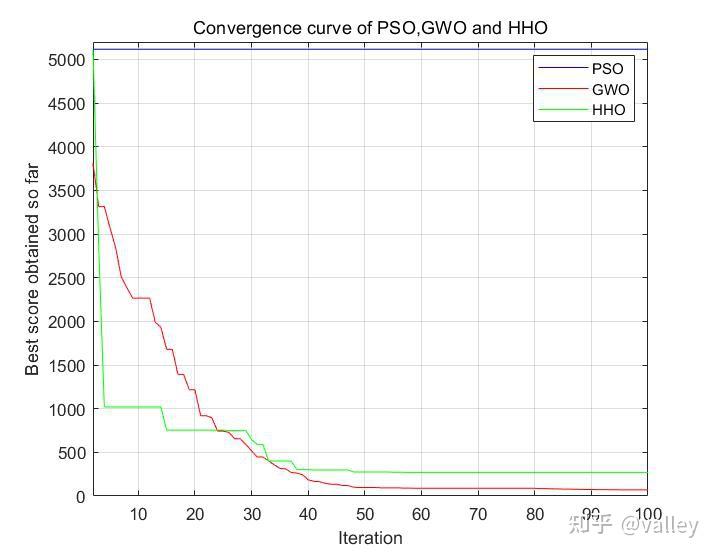
从图10中可以看到这个结果非常离谱。。。我们先看一下原文数据:
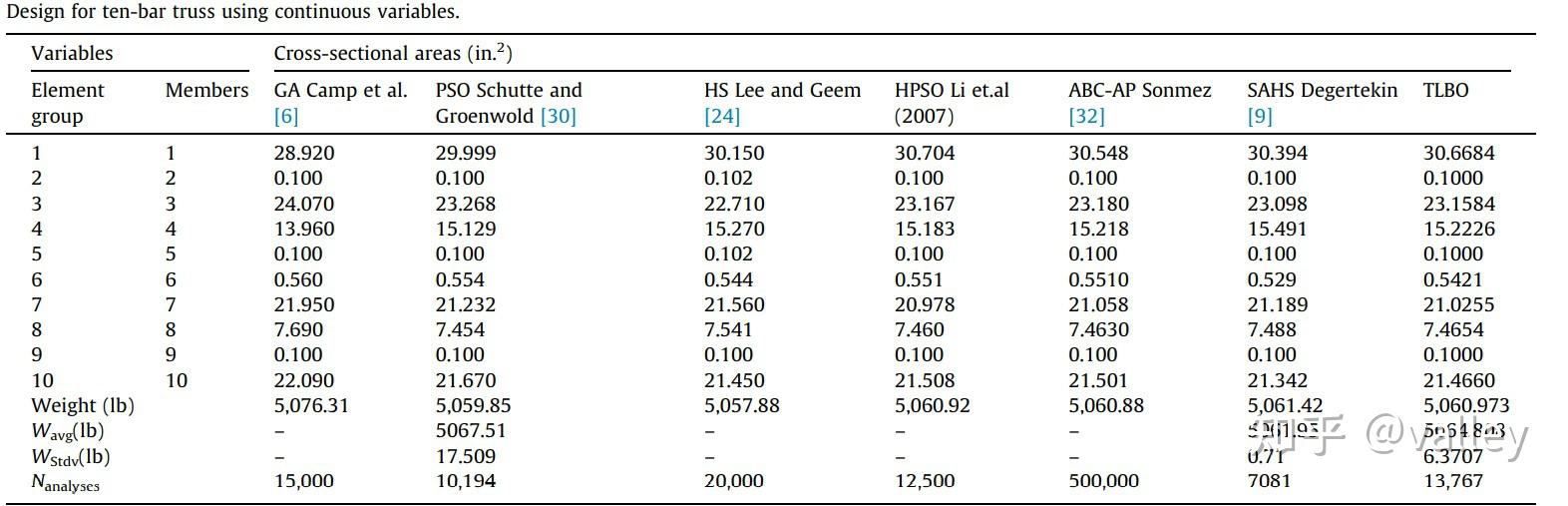
对于不同位置的杆,各算法的优化结果几近相同,可是问题案例中对各参数仅做出了如下解释:
“In this variation of ten-bar truss, cross-sectional areas may vary from 0.1 in.2 to 35.0 in.2 .”
这里并没有提到各杆质量在适应度函数中的权重比,但是从数据中总是感觉有权重这么一回事,所以还有待研究。
总的来说HHO算法对哈里斯鹰的捕食行为模拟的十分真实,虽然在桁架优化问题中表现不如GWO,但实际上在很多测试函数中HHO展现出的性能是非常强的,不得不说HHO算法给了我们很多启发。若是对文章内容有疑问或是个人见解欢迎大家提出